I. Introduction
Housing prices in Korea have gone through a sudden rise during the COVID-19 crisis while Korea’s aggregate income and consumption were greatly dampened by the government’s social distancing policies. It is unexplainable by a standard neoclassical model which predicts that house prices and aggregate income grow at a constant ratio (Chen and Wen, 2017). The breakdown of the supply chain also increased unemployment rate and uncertainties during the pandemic (Auerbach et al., 2021; Kinda et al., 2022).
Closely associated with the sudden formation of housing boom amid the severe economic recession is the conduct of expansionary monetary policies. In March 2020, the Bank of Korea (BOK) lowered the policy rate to 0.75% from 1.25%, and sequentially lowered it to 0.5% in May 2020. During the same period, the Korean government also provided the first round of emergency relief funds. Households were given 40 thousand to 1 million won accordingly to the number of house members. Consequently, the 2020:Q2 saw a rise of 1.5% in consumption from the previous quarter (김미루․오윤해, 2020). Likewise, 93.7% of the COVID-19 relief funds were estimated to have been spent on consumption expenditure (이태석, 2020).
The emerging strand of literature on the political measures during the COVID-19 crisis shed light on the roles of monetary and fiscal policies during the crisis. Auerbach et al. (2021) argue that the fiscal multipliers are larger during the peak of the pandemic crisis. Brzoza-Brzezina et al. (2021) empirically show that the conduct of expansionary monetary policy is recommended when the lock-down policy is optimal. However, Nwogugu (2021) points out to the adverse policy contagion of monetary and fiscal policies during the pandemic insisting that the monetary transmission of the cash stimulus was misdirected creating bubbles in the asset market. Fornaro and Wolf (2020) and Lepetit and Fuentes-Albero (2022) argue that the monetary policy is less likely to be effective once the spread of the virus suppresses demand when the nominal rate is declined near to the zero lower bound (ZLB).
This paper contributes to this line of literature by investigating the role of monetary and fiscal shocks and the endogenous regime switching between two different regimes: non-COVID and COVID. I provide evidence for the impact of the pandemic on the transmission channels of political shocks linked to house prices by examining the state-dependent responses of Korean apartment prices and the policy multipliers on apartment prices. I extend the discussion by matching the pre-and post-COVID periods to the economies with and without the liquidity trap determined by low-interest rates and economic slack.
The empirical results suggest that apartment prices respond positively to the monetary shock, but negatively to the fiscal shock in the COVID regime. The monetary multipliers on apartment prices are larger in the COVID regime while the fiscal multipliers are smaller. The apartment prices respond positively to the monetary shock in the ZLB state and in the economic slack, while it is the opposite for fiscal shock. The estimation of cumulative multipliers also provides consistent results. The major contribution of this paper is that the inclusion of the COVID proxies, namely unemployed, oil price, uncertainty in the local projection (LP) process evidence that the economic state with the pandemic intensifies the ineffectiveness of the monetary policy.
The rest of the paper is structured as follows. Section II discusses the stylized facts. Section III presents the model framework. Section IV provides the main results and Section V presents the results associated with the ZLB and economic slack. Section VI provides the robustness checks and Section VII summarizes the findings.
II.Stylized Facts
The effectiveness of monetary policy at ZLB is widely studied by many researchers (Gambacorta et al., 2014; Inoue and Rossi, 2021; Wu and Xia, 2016). The ZLB on nominal interest rates impedes the transmission channels of monetary policy, particularly when inflation is low (Borio and Hofmann, 2017; McCallum, 1999). There is another interest rate termed the ‘reversal interest rate’ which resembles the property of ZLB. A reversal interest rate is a rate at which the accommodative monetary policy reverses its expected effect and turns contractionary (Brunnermeier and Koby, 2018). Christiano and Eichenbaum (1992) point out that the strong liquidity effect of money shock can drive the nominal rate down by oppressing the inflation premium. However, if the consumption channel is blocked owing to the ZLB, it is predicted that low inflation in a liquidity trap generate asset bubbles. The underlying notions of the ZLB and the liquidity trap are connected to each other as the ZLB is one of the monetary transmission channels inducing the liquidity trap (Ullersma, 2002).
Mertens and Ravn (2014) discuss that the fiscal multiplier is larger at the ZLB state. Likewise, Christiano et al. (2011) and Eggertsson (2009) argue that fiscal multipliers are larger in liquidity traps than in the normal state. Lustenhouwer (2020) argues that fiscal stimulus with government spending is conducive to resolving the liquidity trap. Afonso and Sousa (2009) show that the effect of fiscal shock on house prices is positive and persistent. Ali al-Nowaihi and Dhami (2016) argue that under the possibility of a liquidity trap, the monetary stimulus can soon be exhausted when the discretion on fiscal policy is retained. Woodford and Xie (2022) point out that welfare can be maximized when the monetary and fiscal policies are contemporaneously committed as the ZLB is dissipated. Coenen et al. (2012), Farhi and Werning (2016), and Dime et al. (2021) insist that fiscal multipliers are larger when the government spending is accommodated by the monetary policy or when the nominal rate is near ZLB. (H1) These findings extract a hypothesize that the impact of monetary shock on house prices are more evident than the fiscal shock in the post-COVID with a nominal rate near ZLB.
According to a publication issued by the Korea Institute for Industry Economics & Trade (여유진 외, 2021), the growth rates of household consumption and construction investment fell by 7.4% and 3.4%, respectively after the pandemic. The number of employed decreased by 457 on the basis of 1,000 persons along with a fall in GDP growth rate, 3.7%. The oil markets were severely damaged by COVID-19 and the failure of the oil negotiation between Russia and Saudi Arabia (2020:3-4) (Ma et al., 2021). Amid the heightened uncertainties, the desire to hold nominal liquid assets generates deflationary economic pressures (Haan et al., 2017). Heightened uncertainty raises the land prices while delaying land development (Cunningham, 2006). (P1) This leads to a prediction that the political effects on house prices are altered by the COVID channels as the downward pressures on the nominal rate and the presence of economy slack lead to the distortion of the desired political transmission paths.
III. Model Framework
Jordà (2005)’s LP methodology is widely used in macroeconomic research to estimate impulse responses when the number of variables are limited and when the lag length is misspecified (Adamek et al., 2022; Auerbach and Gorodnichenko, 2013; Born et al., 2019; Jordà & Taylor, 2015). Though the reliability of the LP estimator has been questioned by a few researchers (Brugnolini, 2018; Kilian and Kim, 2011), there are several advantages to using LP (Lof and Nyberg, 2019). First, LP is advantageous when dealing with nonlinearities. Second, LP enables the incorporation of large sets of state variables and high-frequency data. The first step of LP presents ordinary least squares regressions for forecast horizons as specified in <Eq. 1>.
Here, αh are vector constants. are parameter matrices with lag order of p and forecast period of h. The vectors of are heteroscedastic disturbances. A set of regression coefficients are LPs. The slope matrix is the response of yt+h to a shock of reduced form. The simplest approach to measure the state-dependent responses is to use a binary or dummy variable. I employ a logistic function to compute state probabilities as follows.
Here, zt, the change in the endogenous variable at time t is standardized, whereas γ, threshold parameter given by the user is scale-invariant. Regime 1 (R1) and Regime 2 (R2) are determined by F(zt) as R1:y(t−1) • (1−F(z(t−1)) and R2:y(t−1) • 1−F(z(t−1)). The variable zt can be obtained by employing the Hodrick-Prescott (HP) method (Hodrick and Prescott, 1997). In this study, instead of using HP method, I allow a direct application of numeric vector into the logistic function. The coefficient matrices and are obtained from the following LPs in <Eq. 4>.
I modify <Eq. 4> to include a COVID dummy binary variable and the exogenous COVID proxies.
where, y=[apt, policy shock]
Here, <Eq. 1> and <Eq. 5> indicate the linear form and state-dependent regimes, respectively. To calculate the cumulative multipliers of monetary and fiscal policies, I utilize the one-step IV methodology introduced by Ramey and Zubairy (2018).
where, shockt=policyt+h−policyt−1
Here, It is the COVID binary dummy variable, and COt represents a set of COVID proxies. I use the Newey-West correction for standard deviation (Jordà, 2005; Newey and West, 1987). The nominal interest rate, nrt+h−nrt−1 and government spending, gexpt+h − gexpt−1 are the identified shocks. I use the current nominal rate and government expenditure for political shocks. COt−1 shockt−1 indicates the interaction between political shock and the COVID proxies. and indicate the political multipliers on apartment prices in non-COVID and COVID regimes, respectively. Following Kinda et al. (2022), I decompose the trend and cycle components of the COVID proxies to examine the effect of COVID-19 by employing HP-filter. Using trend components allows me to measure the permanent shock of the proxies while isolating the transitory shock of COVID-19.
where, COi,t = ρpCOi,t−1 + ϵi,t
Here, COi,t is the permanent component of the shock with a persistence parameter, ρp · ϵ(i,t) is the permanent shock with and vi,t is the transitory shock with . I set λ = 14,400 to smooth the parameters for monthly data. I use samples of 2015:1-2022:2 given that the last economic cycle of the pre-COVID begins in 2015 and the house prices begin to subside in early 2022 (Figure 1).
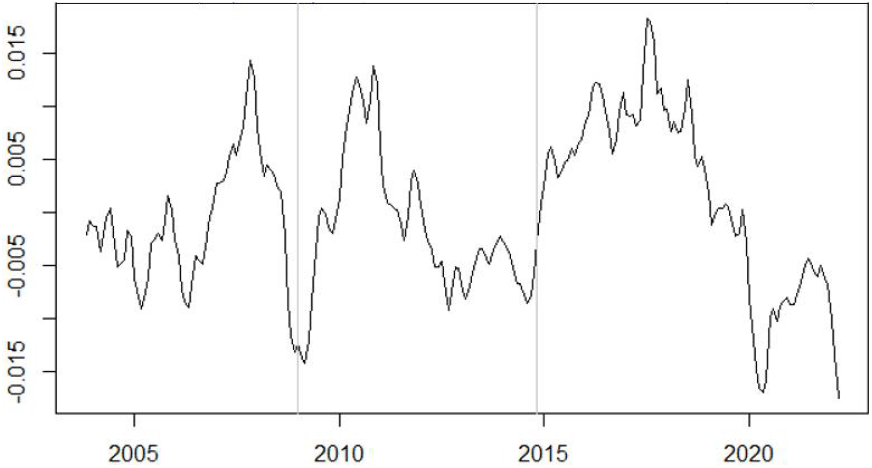
Note: The real GDP in logarithm is smoothed by trend function.
I use the real apartment transaction price index (2017.11=100) for house prices. Apartment prices are seasonally adjusted and deflated by using consumer price index. The yields on 3-year maturity corporate bonds (AA-) and real general government expenditures are used for monetary and fiscal shocks, respectively. The annual data on government expenditures are only available until 2021, thereby I interpolate them into monthly data using the Denton method. The missing data for January, February, and March 2022 are interpolated with the forecast estimates obtained from the vector autoregressive prediction model. The government expenditures are seasonally adjusted and deflated by the GDP deflator. The number of the unemployed and the economic policy uncertainties (EPU) index reported by Korea Development Institute (KDI) are used for unemployment and uncertainty, respectively. The crude oil price denominated in the nominal dollar is used for the oil price. All the data except EPU are collected from the economic statistics system (Table 1). I estimate the persistence parameters of COVID proxies by regressing the permanent components on its lag. The variance of the permanent components is obtained by (Contreras and Nichols, 2010). In the COVID regime, the variations of both trend and cycle components are the highest in oil price at 0.04 and 0.129, while the trend component of uncertainty has the largest variation with a 0.022 standard deviation in the non-COVID regime (Table 2). The persistence parameter of the oil prices is the highest, 0.9 with a 4.4% standard deviation. The persistence parameters of the unemployed and uncertainty are 0.59 and 0.65 with standard deviations of 2.6% and 9.7%, respectively (Table 3).
p-value indicates the result of T-test of difference in means of COVID proxies in COVID and non-COVID regimes.
| COVID proxies | Persistence (ρ) | S.D. (σϵ) |
|---|---|---|
| Unemployed | 0.589 | 0.026 |
| Oil price | 0.859 | 0.044 |
| Uncertainty | 0.646 | 0.097 |
IV. Main Results
This section provides the main results of the impulse responses matrices and cumulative political multipliers when there is a 1 standard deviation shock (∓1σ) of innovations. LP system in this study consists of two endogenous variables, namely apartment prices and policy shocks, and three exogenous variables, the number of unemployed, oil prices, and uncertainties. The lag orders of 1 are selected for both endogenous and exogenous variables based on BIC. The COVID binary variable is used for switching data. The value ‘0’ is given to periods spanning from 2015:1-2019:12, whereas ‘1’ is given to 2020:1-2022:2. As the first COVID case was reported in January 2020 in Korea, I set 2020:1 as the period division.
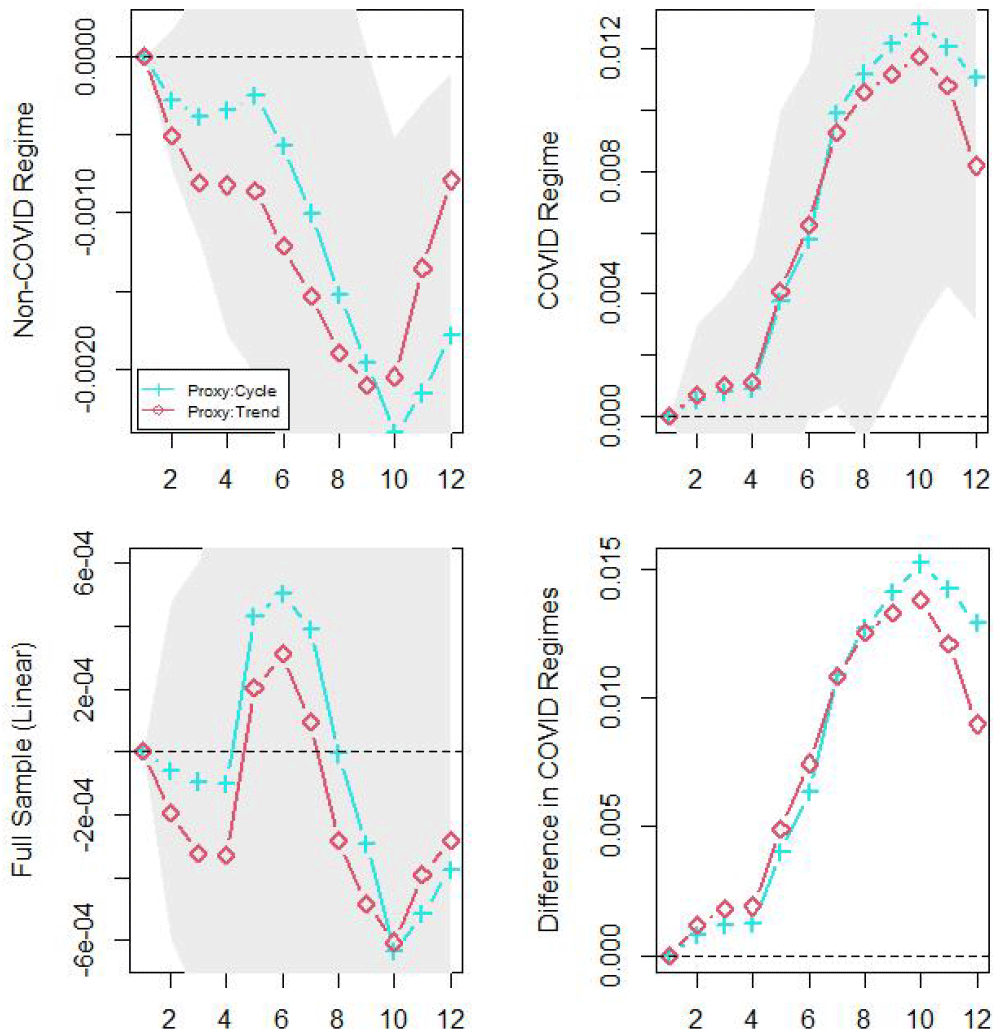
<Figure 2> presents the impulse responses of apartment prices to monetary shocks using cycle and trend components of the COVID proxies. In line with the literature, accommodative monetary policy has a positive and significant effect on apartment prices in the COVID regime, whereas the effect is negative in the non-COVID regime. Additionally, the cycle components of the COVID proxies affect more positively the apartment prices than the trend components in the COVID regime after 7 months. Considering the political implementation and transmission lags of the COVID effect, the results go align with the prediction. The responses of cycle and trend components in the COVID regime peak around 0.014 and 0.012, respectively. In the non-COVID regimes, the troughs of the cycle and trend components are around −0.004 and −0.0025, respectively. Contrary to the regime-dependent responses, 1 peak with 2 troughs are found in the full sample (linear) suggesting that nonlinearity exists in the time-series data of nominal rates and apartment prices. Differences in the impulse responses of COVID and non-COVID regimes get larger between the cycle and trend components after 8 months implying that it takes approximately 8 months for the interaction of the monetary shock and COVID shock to transmit into the apartment prices. The differences are obtained by subtracting responses of non-COVID regime from the COVID regime.
<Figure 3> depicts the impulse responses of apartment prices to fiscal shocks using cycle and trend components of the COVID proxies. In line with literature, the apartment prices with cycle component channels react negatively to the fiscal shocks in the COVID regime, but positively in the non-COVID regime. Such a finding suggests that the liquidity offered by the conduct of fiscal policy flows more into the productive sector during the bad times than during the good times. The impulse responses with cycle components peak at 0.002 in the non-COVID, while hitting the trough of −0.001 in the COVID regime. Contrarily, the apartment prices with trend components react positively to the monetary shocks both in the COVID and the non-COVID regimes. The impulse responses with trend components peak around 0.001 and 0.003 in non-COVID and COVID regimes, respectively. The responses presented in the full sample panel suggest that the transitory effects of the unemployed, oil prices, and uncertainty accelerate the positive transmission of fiscal shocks to the apartment prices.
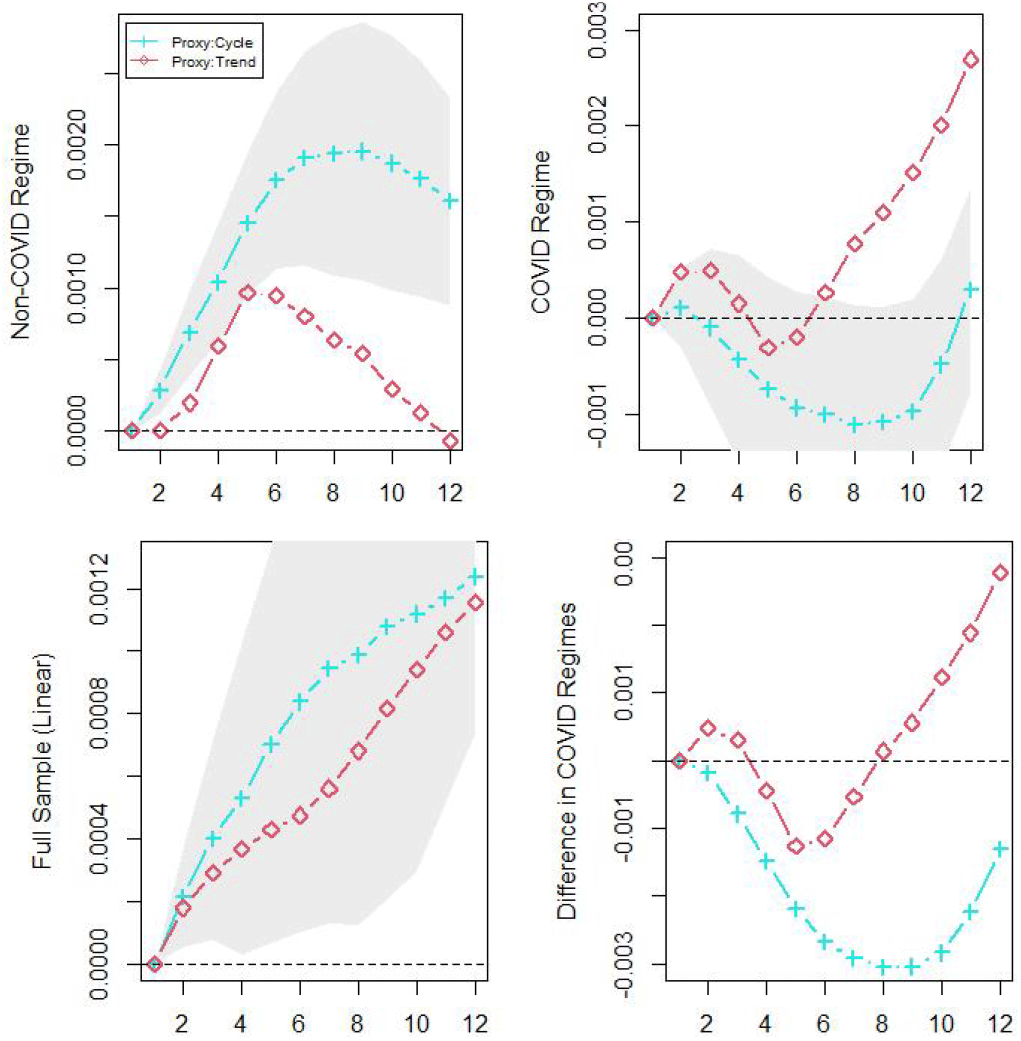
<Figure 4> summarizes the cumulative monetary multipliers on apartment prices. Consistent with the response matrices, the monetary multipliers with both the cycle and trend components of the COVID proxies are positive in the COVID regime peaking 0.05, whereas those in the non-COVID regime are negative, troughs at −0.055. These findings imply that the role of nominal interest rate became reinforced in the post-COVID as house prices react increasingly more sensitively to the changes in nominal rates.
Note: Monetary multipliers of cycle components (left) and trend components (right). The shaded regions and dashed lines are corresponding 95% confidence intervals.
<Figure 5> summarizes the cumulative fiscal multipliers on apartment prices. Consistent with the impulse response matrices, the fiscal multipliers of COVID proxies are negative in the COVID regime but positive in the non-COVID regime. Contrarily, those with the trend components are positive in the COVID regime but negative in the non-COVID regime. Consistent with Afonso and Sousa (2009)’s finding, the cumulative fiscal multipliers of the linear function with full sample (2015:1-2022:2) evidence that the effect of government spending on apartment prices are positive and persistent.
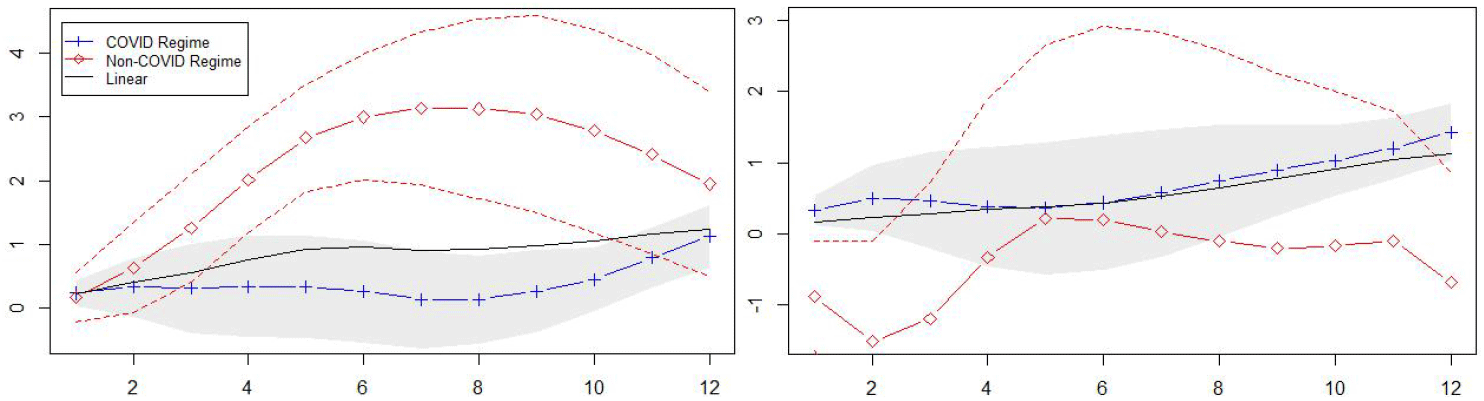
Note: Fiscal multipliers of cycle components (left) and trend components (right). The shaded regions and dashed lines are corresponding 95% confidence intervals.
V. Economic Regimes with Zero Lower Bound (ZLB) and Economic Slack
This section explores the effects of ZLB state and economic slack on the political transmission to the apartment prices using CB yields and real GDP as switching data. To match the regime switching between the ZLB state and the normal state with the pre-and post-COVID periods, I use the sample spanning from 2017:4-2022:2. As shown in <Figure 6>, regime 2 of ZLB state (γr < 2.2) almost corresponds to the post-COVID periods with a few negligible deviations. To match the economic regimes with the COVID regimes, I use the full sample spanning from 2015:1-2022:2. As depicted in <Figure 6>, though the regime of economic slack does not perfectly corresponds to the COVID regime (2020:1-2022:2), the periods spanning from 2020:1-2021:2 fall into the regime 2 (γgdp > −0.0032) with economic recession. The threshold parameters are obtained by regressing the production index on the apartment prices using threshold regression.
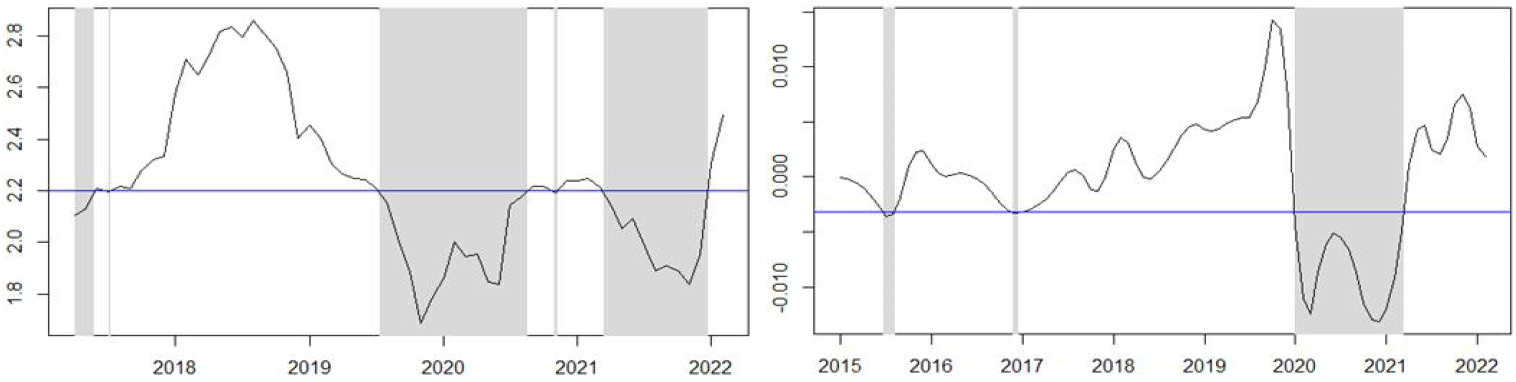
Note: Thresholds of CB yield with first differentiation (left, γr = 2.2) and cycle components of real GDP (right, γgdp = −0.0032). The blue line is the threshold obtained by regressing production index on apartment prices. The F(z) estimates are 0.047 and 0.5. The shaded areas indicate regime 2 where the estimates are below the thresholds.
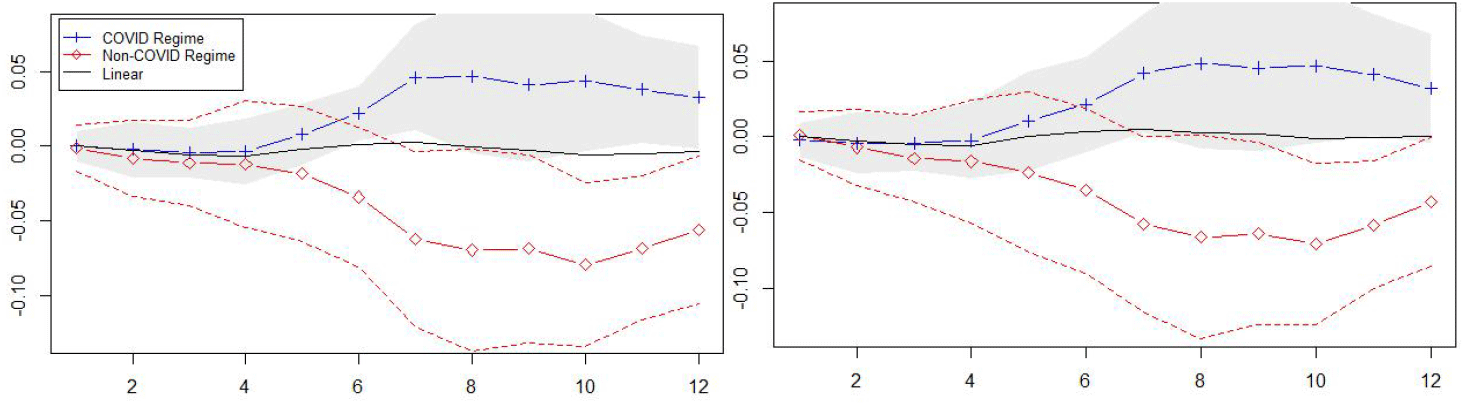
<Figure 7> illustrates the cumulative monetary and fiscal multipliers on apartment prices with cycle components of the COVID proxies in ZLB and normal states. In line with literature, the monetary multiplier on apartment prices is, in general, larger at ZLB than in the normal state as the monetary multiplier at ZLB (blue) is persistently located above the average (linear) monetary multiplier (black) after 2 months (h=2). Also consistent with literature, the fiscal multiplier on apartment prices is, in general, smaller at ZLB than in the normal state as the fiscal multiplier of ZLB (blue) is persistently located beneath the average monetary multiplier (black) after 3 months (h=3).
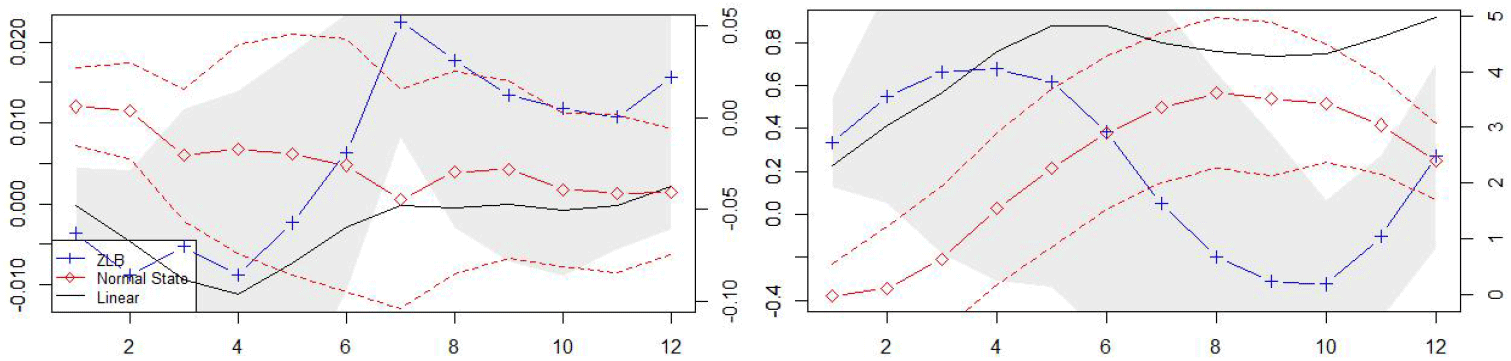
Note: Monetary multipliers (left) and fiscal multipliers (right). The scale of zero lower bound and linear multipliers (left axis) and the scale of normal state multiplier (right axis).
Similarly, the movements of cumulative monetary multipliers depicted in <Figure 8> suggest that monetary multipliers on apartment prices are larger in the economic slack than in the normal state, whereas the fiscal multipliers are smaller in the economic slack than in the normal state. These findings are in parallel with the hypothetical prediction that the impact of monetary policy on apartment prices is larger than the fiscal policy during the economic recessions when the nominal rate is determined near ZLB generating a liquidity trap.
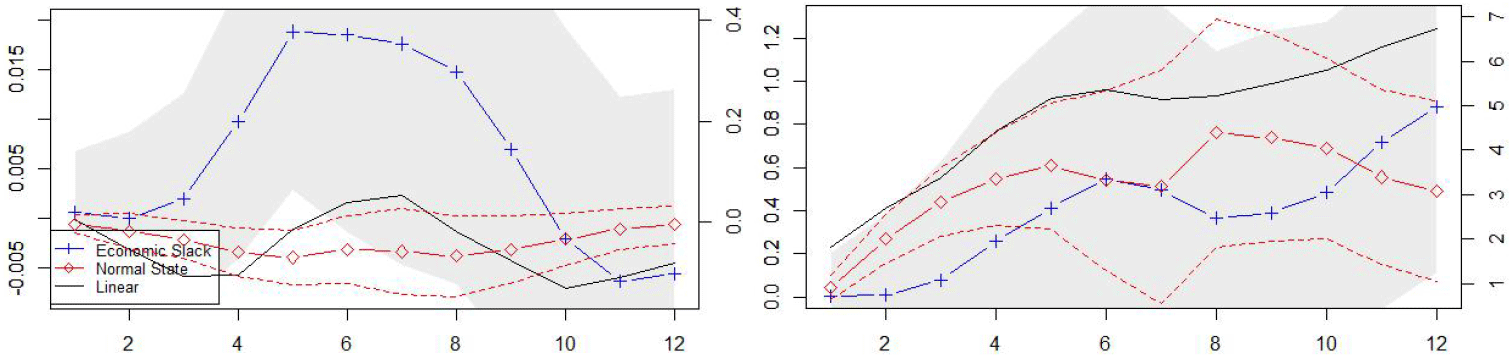
Note: Monetary multipliers (left) and fiscal multipliers (right). The scale of economic slack and linear multipliers (left axis) and the scale of normal state multiplier (right axis).
VI. Robustness Checks
This section examines the sensitivity of impulse responses and the cumulative political multipliers by allowing some changes to the LP system. In the previous sections, I used the direct logistic functions to switch the regimes with a specific threshold parameter determined at γcovid=0.5. In this section, I use the HP-filter to decompose the series of numeric vectors of the switching data (COVID dummy variables) by setting λ=129,600 as suggested by Ravn and Uhlig (2002). I also compare the results when trend is considered (trend=1) and not considered (trend=0). <Figure 9> illustrates the impulse responses of apartment prices to political shocks with cycle components of COVID proxies. Consistent with the previous results, the apartment prices respond positively to the nominal rate shock, but negatively to the government spending shock in the COVID-regime. The responses are opposite in the non-COVID regime. The apartment prices respond less sensitively to the unexpected external shocks when trend is considered indicating that the inclusion of trend factor renders prices to deviate less from the trend. The political multipliers depicted in <Figure 10> also suggest that the impact of monetary shock on apartment prices is positive, but fiscal shock on apartment prices is negative in the COVID regime. The opposite results are illustrated in the non-COVID regime.
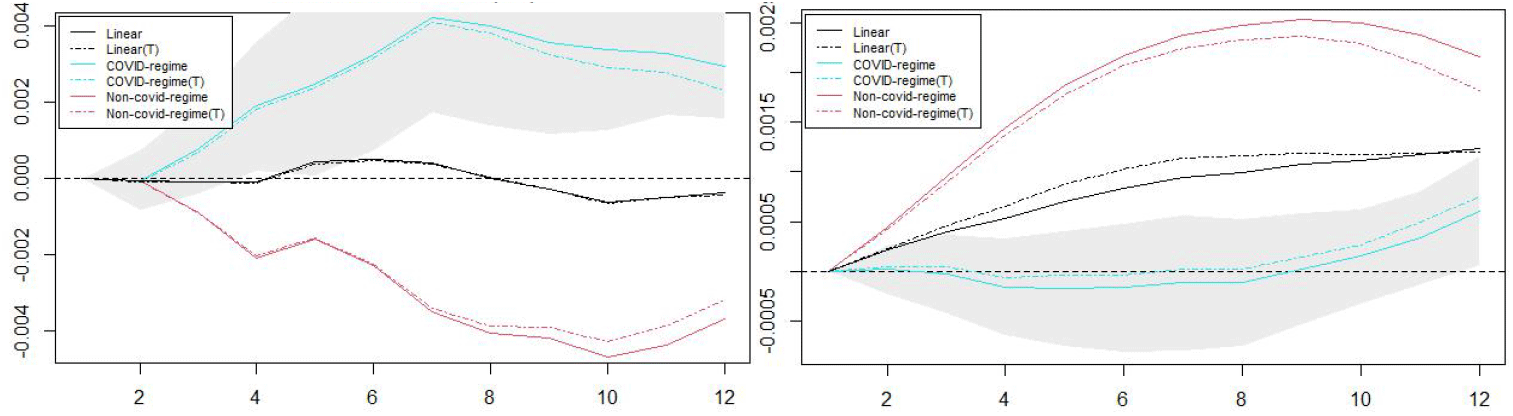
Note: Impulse responses to monetary shock (left) and fiscal shock (right). The dashed lines indicate trend considered (trend=1).
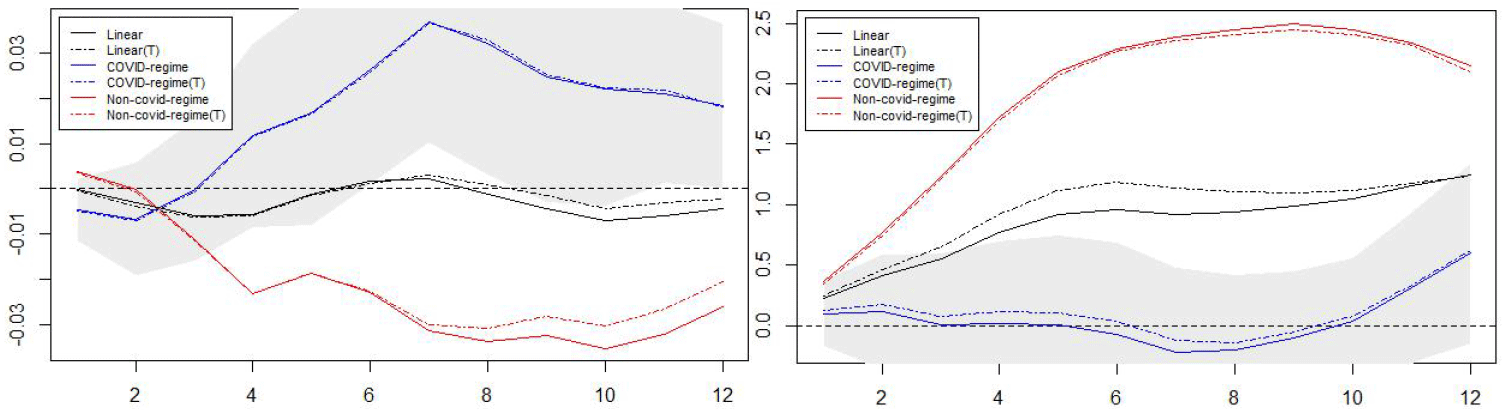
Note: Monetary multipliers (left) and fiscal multipliers (right). The dashed lines indicate trend considered (trend=1).
VII. Conclusion
The Korean government sought to defend against a pandemic-driven recession by lowering nominal rate and allocating emergency relief funds. Nevertheless, as extensive literature on economic policies suggests, the monetary policy is less likely to be effective in directing liquidity into the productive sector during the crisis merely creating asset bubbles, while the assessment on the fiscal policy is readily positive. This paper explores the multiplier effects of monetary and fiscal policies on Korean house prices during pre-and post-COVID periods. I employ Jordà (2005)’s LP methodology to construct state-dependent impulse response models and include the proxies explaining the impact of COVID-19 on the economy.
The empirical results suggest that in line with the literature, the impulse responses of apartment prices to 1 standard deviation (−1σ) monetary shock is positive (0.014) in the COVID regime (It), but negative (−0.0025) in the non-COVID regime (1‒It). Contrarily, the effect of 1 standard deviation fiscal shock (+1σ) on apartment prices is negative (−0.001) in the COVID regime, but positive (0.002) in the non-COVID regime. Moreover, the transitory shock of exogenous COVID proxies, namely the unemployed, oil prices, and uncertainties intensifies the political effects on apartment prices. Consistent with the impulse responses, the cumulative monetary multipliers on apartment prices are positive (0.05) in the COVID regime, while negative (−0.055) in the non-COVID regime. The results of cumulative fiscal multipliers are the opposite, 0 and 3 in the COVID and non-COVID regimes, respectively (the values in the parentheses are either peaks or troughs).
Additional analysis on the political transmission in the economy with a liquidity trap suggests that monetary multiplier on apartment prices is higher when the nominal rate is near ZLB (γr < 2.2) and when there is economic slack (γgdp < −0.0032), while the fiscal multipliers on apartment prices are estimated to be higher in the normal states. The conduct of robustness checks using HP-filter decomposition as an instrument to switch the regimes present consistent findings with the main results. Additionally, the inclusion of trend (trend=1) suggests that the responses in the non-COVID and COVID regimes deviate relatively less from the average (linear) responses compared to when the trend is not considered. These empirical findings highlight the importance of optimal discretion on monetary and fiscal policies in terms of minimizing the ineffectiveness of the political instrument, which may otherwise worsen the imbalance and decoupling of the real economy and the asset market during the bad times.