I. Introduction
Korea already has the basic framework of the multi-pillar retirement income guarantee system that consists of public and private pensions, but both public and private pensions have not been introduced long ago, so they are still in an immature stage. Considering the reality of Korea’s retirement income guarantee system, the housing pension (reverse mortgage for elderly homeowners) system was introduced in 2007 as a supplementary pension system that can supplement the insufficient public and private pension systems, followed by the farmland pension (reverse mortgage for elderly farmland owners) system in 2011. The level of monthly payments in Both housing and farmland pensions is determined in proportion to the value of the real estate (housing and farmland), which is collateral. Therefore, because the housing value in rural areas is relatively low, even if elderly farmers use housing pensions, it was still difficult to raise living expenses. On the other hand, looking at the asset structure of the elderly farmers, the value of the house they own was very low, but they own farmland with a relatively high value. Therefore, the government decided to introduce the farmland pension system, a reverse mortgage for farmland owners, to improve the life of elderly farmers and it was implemented in 2011. The number of new pensioners to the farmland pension increased rapidly every year starting with 911 at the end of 2011, and as of September 30, 2020, 16,769 elderly people were enrolled. And the average age of pensioners was confirmed to be 73.8 years. The average price of collateral farmland was around KRW 180.1 million, and the average monthly payment of the farmland pension was confirmed to be KRW 925,780 (Lee et al., 2020). As such, the farmland pension is a policy pension product developed to support the stabilization of elderly farmers in rural areas. Considering the demographic structure, demand is expected to continue to increase in the future. At the time of introduction, the farmland pension was designed to have an actuarial structure similar to that of the housing pension. In other words, the level of monthly payment of the farmland pension is determined under the condition of equivalence that satisfies the size of the expected loss (PVEL) is equal to the size of the expected guarantee premium (PVEW), as in the case of the housing pension1). However, as is well known, most of the main variables such as farmland price, loan balance, loan termination probability, and loan survival probability, which are applied to the basic actuarial model of farmland pension, are stochastic variables. Nevertheless, when determining the level of monthly payments using the basic actuarial model, the average value of these variables is applied and calculated for convenience of calculation. Therefore, even if the condition of equivalence is satisfied in the basic actuarial model, considering that farmland pension is a long-term financial product, in the real world, the values of the main variables may deviate greatly from the average values assumed and as a result, we can face the situation that the condition of equivalence is not satisfied.
As a result of actual operation, if the result of PVEL>PVEW occurs, the farmland pension guarantor will suffer a loss equal to PVEL-PVEW, and if the result of PVEL<PVEW occurs, the farmland pension guarantor will see a profit equal to PVEW-PVEL. In fact, the satisfaction of the PVEL=PVEW condition under the current basic actuarial model means that the probability that the guarantor will lose (i.e., the probability that the result of PVEL>PVEW) and the probability of profit (i.e., the probability that the result of PVEW>PVEL) are equal at 50% respectively.
In this study, we want to check if the condition of equivalence (PVEL=PVEW) will be satisfied when the monthly pension amount determined by the current basic actuarial model is paid for life, by evaluating the stochastic process of main variables applied to the basic actuarial model of farmland pension. If the condition of equivalence is not satisfied, we want to check the level of monthly payment (hereinafter referred to as “fair price”) that can satisfy the condition when evaluated through realistic analysis considering the stochastic process of main variables. Subsequently, this study intends to evaluate the expected rate of return of farmland pensioners and evaluates the expected rate of return separately in the case where the monthly payment determined by the current basic actuarial model is paid and in the case where the fair price is paid. The fair price of farmland pensions presented through the analysis of this study could help farmland pension providers improve their products in the future. The expected rate of return evaluated and presented in this study is an evaluation indicator that is attempted for the first time about farmland pension and makes it possible to compare farmland pension with other pension products (e.g., immediate annuity or housing pension). So, it is expected that it can be a useful indicator that can help consumers determine the final choice of product. The structure of this study is as follows. Following the introduction of Chapter I, Chapter II discusses the method of determining the price of farmland pensions and evaluating the expected rate of return, and Chapter III describes the data and analysis methodology to be used for the analysis of this study. Chapter IV presents the analysis results of this study, and Chapter V presents the conclusions of this study.
II. Pricing Method and Expected Rate of Return of Farmland Pension
Pricing of farmland pension (calculation of monthly payment amount) in the basic actuarial model is carried out in the process of finding the level of the monthly payment that satisfies the condition of equivalence that the present value of the expected loss (PVEL) and that of the expected guarantee premium (PVEW) has the same value. PVEL and PVEW are calculated as <Eq. 1> and <Eq. 2>, respectively.
In <Eq. 1>, PVEL is the present value of the expected loss; T(x) is the period left until the maximum lifespan; Bt is the outstanding loan balance at time t; Lt is the farmland price at time t; is the loan termination probability; i is the expected interest rate.
In <Eq. 2>, PVEW is the present value of the expected guarantee premium; wt is the guarantee premium at time t; is the loan survival probability.
At the time of introduction, the basic actuarial model of the farmland pension was designed in a similar form to the housing pension, but since its launch, both the housing pension and the farmland pension have been slightly modified according to their respective needs. In this relationship, some differences between the two programs that are currently noticeable can be identified as follows. First, in the housing pension, when creating the loan termination probability and the loan survival probability, the method of applying the mortality rate was changed from the initial female mortality rate to the method of applying the multiple mortality rate. But, in the farmland pension, the method of applying the female mortality rate is still maintained. Second, in the housing pension system, 1.5% of the current home value is charged as an initial guarantee premium at the time of loan initiation, and 0.75%/12 of the loan balance is charged as a monthly guarantee fee after loan commencement. On the other hand, in farmland pension, an initial guarantee premium was imposed at the time of launch, but after that, the initial guarantee fee was abolished and only 0.5%/12 of the loan balance is currently charged as a monthly guarantee fee.
The fixed monthly payment of the farmland pension is determined as shown in <Eq. 3> by applying the maximum loan limit that can satisfy the condition of equivalence (PVEL=PVEW).
In <Eq. 3>, a is the fixed monthly payment; PL is the maximum loan limit; j is the monthly guarantee premium rate.
After determining the level of the monthly payment that satisfies the conditions of equivalence (PVEL=PVEW) in the basic actuarial model of farmland pension, when the amount determined in this way is paid until the loan is terminated, the condition of equivalence in the basic actuarial model may not be satisfied in the real world. This is because the values of the main variables applied to the calculation of <Eq. 1> to <Eq. 3> above are all fixed values, but most of the main variables are stochastic. Therefore, to evaluate if the equivalence condition in the actuarial model is satisfied in the real world, it is necessary to evaluate through realistic analysis considering the stochastic process of the main variables applied to the basic actuarial model. We will discuss this later in Section 3.
The pensioner’s expected rate of return (ERR) is the value that could satisfy the condition that the cumulative present value of both monthly payments and monthly guarantee premiums at each time point until t=N and the present value of the pensioner’s debt at t=N becomes equal as we can see in <Eq. 4>2).
In <Eq. 4>, LN is farmland price, ft is risk-free interest rate at time t; y is the expected rate of return.
We will first evaluate the value of ERR at a future specific time point (t=N) based on the pensioner’s life expectancy. Plus, we also try to evaluate the values of ERR at time point t=24, t=120, t=life expectancy*1.4, and at the time point when pensioner becomes age 111 (that is the maximum life span) to confirm the changing pattern of ERR.
We can calculate the ERR at each time point we want to get through the Monte Carlo simulation analysis and optimization process which considers stochastic processes of main variables.
Farmland Pensioners have ownership of the farmland until the loan is terminated, so they can generate additional income through self-cultivation or renting. Assuming that a lease is made, the farmland pensioner’s expected rental rate of return for each evaluation time point (N) can be obtained by calculating the geometric average return of the rental rate of return as shown in <Eq. 5>.
In this occasion, because the rental rate of return at time t is a stochastic variable, we first generate the probability distribution of geometric average rates of return at each time point (t=N) by using Monte Carlo simulation analysis. And then we use the median value on the probability distribution as the expected rental rate of return.
In <Eq. 5>, E(N) represents expected rental rates of return at t=N; kt is the forecasted future value of rental rates of return at time t.
To compare the values of rental rates of return evaluated at each time point, we must build appropriate stochastic models to forecast the stochastic variables used in each calculation formula.
In the case of housing pension, previous studies that evaluated guarantor’s risk through concurrent simulation analysis reflecting the stochastic process of main variables include studies such as Lew and Ma (2015) and Ma and Yoo (2023). To evaluate whether the farmland pension is actuarially fair, it is also necessary to analyze the stochastic process of the main variables applied to the farmland pension actuarial model. So, it is analyzed by adopting a concurrent simulation methodology like that of previous studies. When considering the stochastic process of main variables, the sizes of PVEL and PVEW can be evaluated as <Eq. 6> and <Eq. 7>, respectively3).
In <Eq. 6> and < Eq. 7 >, is risk free interest rate at t=α.
To calculate and considering the stochastic process of main variables, it is necessary to establish a forecasting model for generating the stochastic process of each of the farmland price increase rate, risk-free interest rate to be applied as a discount rate, and mortality rate. The size of the guarantor’s net liability (NL) can be evaluated by Monte Carlo simulation analysis using the estimated parameters of the forecasting models. The size of the guarantor’s net liability can be expressed as follows.
Where is the guarantor’s net liability.
This study will evaluate the actuarial fairness of farmland pensions using the probability distribution of generated by Monte Carlo simulation analysis. To say that the farmland pension is actuarially fair, the median value (or average value) of the probability distribution of the must be zero.
To determine the reasonable price of the farmland pension, it will be necessary to first determine the probability of the guarantor’ net liability and then based on this, the final level of monthly payment could be determined.
III. Data and Methodology
Related to simulation studies in mortgage finance, GBM (geometric Brownian motion) model has been used as a main forecasting model when forecasting housing prices or farmland prices. In our analysis, we also use the GBM model to forecast future farmland prices. The GBM model is the model which has a multiplicative random walk process as expressed as in < Eq. 9 > (Charnes, 2012).
In < Eq. 9 >, Lt is farmland price at time t; μ is the rate of return parameter stated on an annual basis; α is the volatility parameter stated on an annual basis; δ is the time step; and Z is a standard normal random variate.
Ma (2021) estimated the parameters of the GBM model to forecast the farmland price using the weighted average farmland price index generated from the price increase rate of paddy fields and dry fields from 08. 2009 to 07. 2020 of the Korea Real Estate Board DB. <Table 1> shows the parameter estimation results of the GBM model reported by Ma (2021). In this study, the same parameters as in <Table 1> will be applied and analyzed when conducting the Monte Carlo simulation by the GBM model.
| μ | σ | |
|---|---|---|
| From 08. 2009 to 07.2020 | 0.0234 | 0.0032 |
To estimate the average rental cost by the price of farmland, Ma (2021) used the 2019 year of rent paid to farmland owners by farmland banks in the lease consignment project implemented as part of the farmland bank project by the Korea Rural Community Corporation. In addition, the appraisal price and area of farmland by category from the 1,760 farmland pensioners’ data from 10.2019 to 09. 2020 was confirmed. As a result of the analysis, the weighted average annual rent for farmland with a price of 100 million KRW was estimated at 338,275 KRW.
On the other hand, as a result of analyzing the rental cost of the rental consignment business using data from 2007 to 2019, it was confirmed that the time series of rental costs follow the form of an additive random walk with a drift. The drift (annual average change) was estimated to be 5.5833, and the volatility was estimated to be 13.5476. Based on this, Ma (2021) established a forecast model such as < Eq. 10 > and used it to forecast the future stochastic process of the annual rental cost.
In < Eq. 10 >, lt is the rental cost at time t; N(0, 1) is a standard normal random variate.
In this study, we will use the same forecasting model < Eq. 10 > as in Ma (2021) for Monte Carlo simulation analysis. The forecasted annual rental rate of return at future time points can be obtained as a ratio of rent to farmland price.
We use the exponential Vasicek model, the mean-reverting interest rate model, to forecast future stochastic processes of the log-transformed 10-year maturity government bond rate (Black and Karasinski, 1991). The exponential Vasicek model we used in our analysis can be expressed as in < Eq. 11 >.
In < Eq. 11 >, ft is log-transformed 10-year maturity government bond rate at time t; κ is the speed of reversion; μ is the mean reversion level of processes; αf is the volatility of processes; εt is a standard normal random variable.
Ma (2022) estimated the parameters of the exponential Vasicek model by the maximum likelihood estimation method using log-transformed 10-year government bond yield data from 01. 2009 to 05. 2021, and the estimation results are shown in <Table 2>.
| κ | μ | σf | |
|---|---|---|---|
| From 01. 2009 to 05.2021 | 0.1695 | 0.9862 | 0.1989 |
In the analysis of this study, when forecasting the stochastic process of risk-free interest rates, the estimation parameters in <Table 2> will be applied and analyzed.
To consider the effect of reducing mortality over time in the analysis, this study used the Lee-Carter model to generate cohort mortality by the cohort life table. To create the stochastic process of the mortality rate using the Lee-Carter model, this study reflected the characteristics of the mortality index time series which showed the ARIMA (1, 1, 0) process. So, the forecasting model of the mortality rate was set up as follows.
Where q(x,t) is the mortality rate in year t for age group x, ax is a constant reflecting the average of the mortality rate time series by age group x, bx is the relative speed of change in mortality index by age group x, c is the constant term of ARIMA(1,1,0) process of kt time series, kt is the mortality index in year t, ϕ is the estimated coefficient of dk(t-1),σ is the volatility of time series, ϵt is a standard normal random variable: N(0,1).
This study used female mortality data from 1970 to 2019 in the Statistics Korea DB for Lee-Carter model analysis. In this study, the maximum lifespan was assumed to be 111 years old. Related this, first, based on the pattern of the difference in the mortality rate for each age from 91 to 99 in 1970 and 2019 among female mortality data from Statistics Korea, the mortality pattern from 100 to 110 was generated through regression analysis. Finally, using the estimated annual improvement rate (rx) of mortality rate after the age of 100 in 1970 and 2019, the mortality rate after the age of 100 in from 1971 to 2018 was generated.
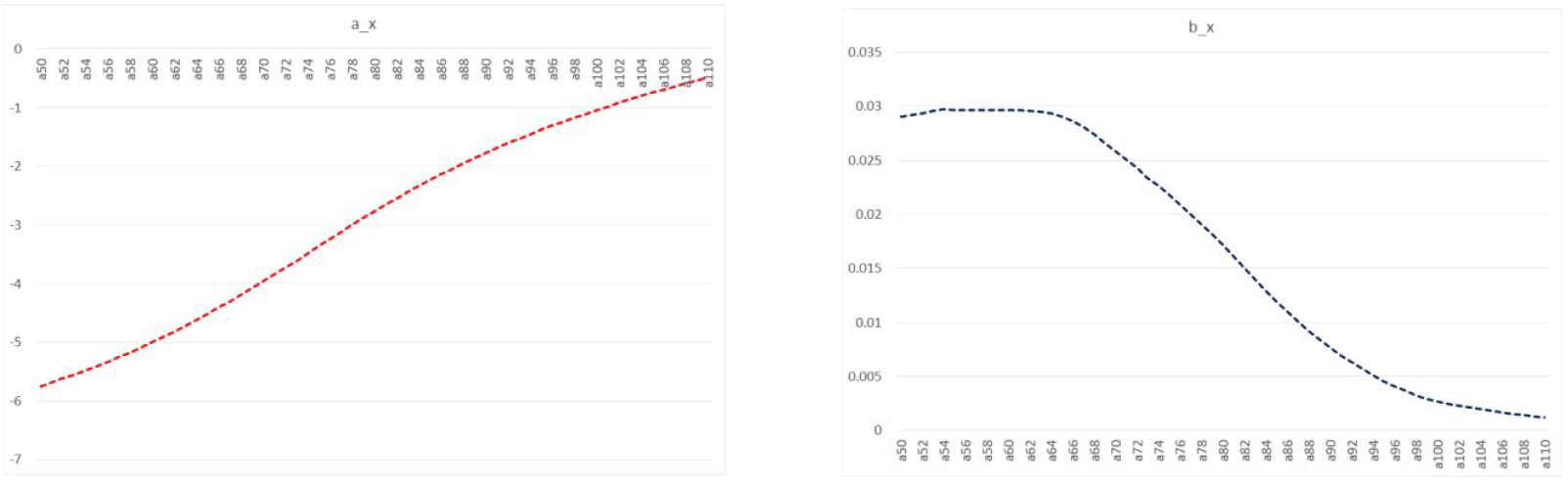
To generate the stochastic process of cohort mortality, this study used the Lee-Carter model to forecast the female mortality rate from age 50 to 110 in each year from 2020 to 2100 using the female mortality rate from 1970 to 2019. <Figure 1> shows the estimated values of ax and bx by age in the Lee-Carter model. Here, the result that satisfies the condition of could be confirmed.
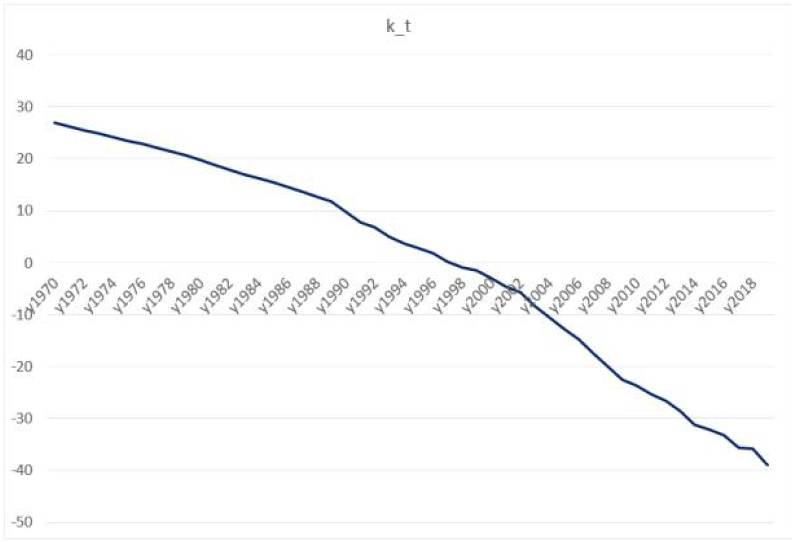
<Figure 2> shows the estimated kt time series from 1970 to 2019 in the Lee-Carter model. Here, too, it was confirmed that the analysis result satisfies the condition of .
Using the estimated values of ax and bx for each age and the forecasted value of time series after 2020, the annual mortality rate after 2020 can be forecasted. For the time series from 1970 to 2019, the ARIMA (1,1,0) model was identified as an appropriate model, and the parameter estimation results are shown in <Table 3>.
|
dkt=−0.8776+0.36908dkt−1+ϵt S.E.: (0.2174) (0.1481) |
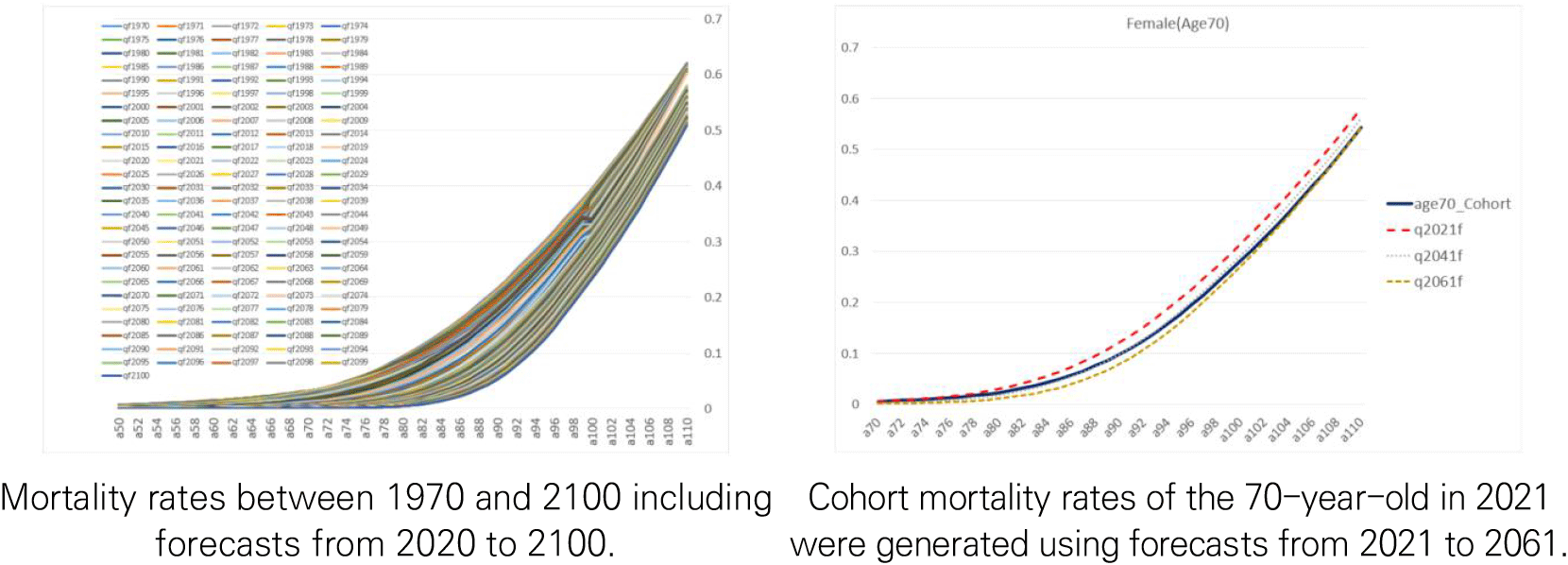
<Figure 3> exemplifies the forecasted female mortality rate (2020-2100) and the cohort mortality rate of a 70-year-old woman in 2021 generated using the forecasted value.
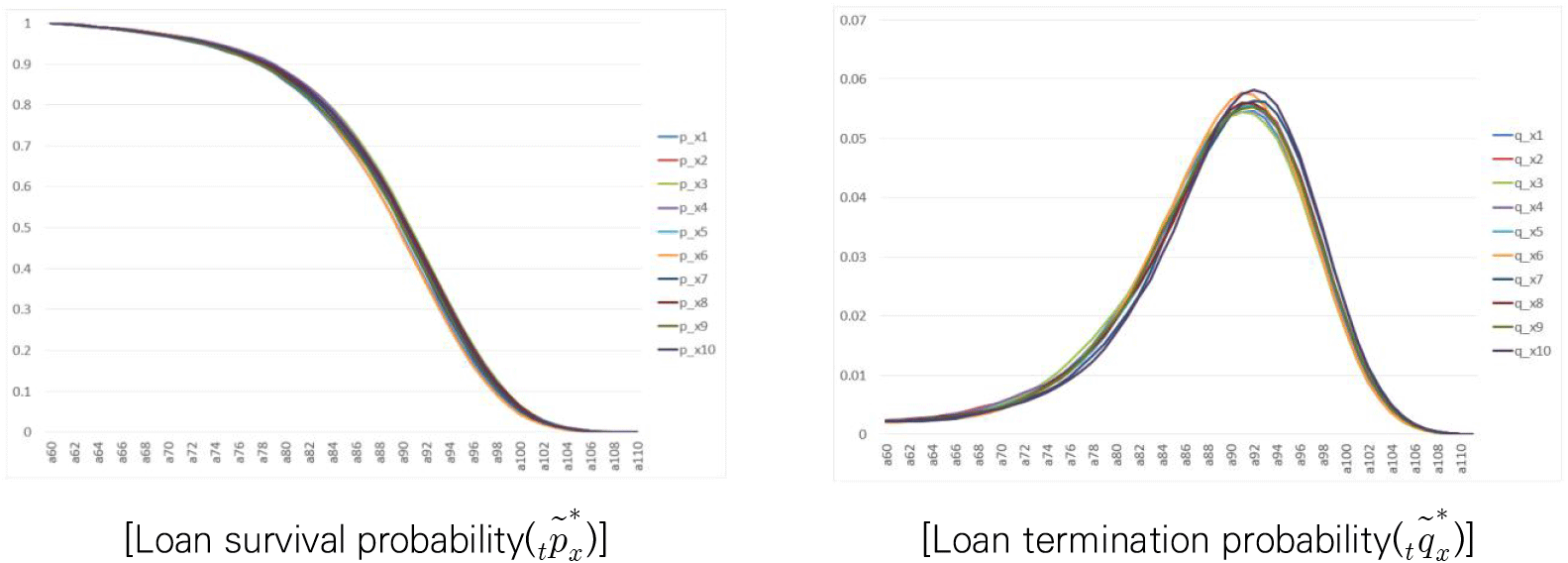
Using the estimated parameters and volatility of the ARIMA (1,1,0) model in Table 3, we can set the forecasting model of the k_t and generate the stochastic process of time series from 2020 to 2100, then finally the stochastic process of loan survival and loan termination probability which can be used in the Monte Carlo simulation analysis can be generated. <Figure 4> illustrates the stochastic process of the loan survival probability and loan termination probability reflecting the cohort effect generated by the Monte Carlo simulation with 10 trials, respectively, in the case of a 60-year-old.
IV. Results of the Analysis
<Table 4> shows the results of evaluating the magnitude of risk that the guarantor may suffer when the monthly payment calculated by the current farmland pension basic actuarial model is paid.
| Age | pmt |
Prob. |
|||
|---|---|---|---|---|---|
| Lower | Median | Upper | |||
| 60 | 311,090 | −6,016,258 | −4,738,076 | −3,459,983 | 0.0000 |
| 70 | 388,290 | −3,147,836 | −2,515,314 | −1,817,815 | 0.0000 |
| 80 | 518,080 | −1,061,171 | −790,068 | −456,401 | 0.0000 |
Note:
Farmland price is assumed 100 million KRW (appraised value).
The level of the monthly payment by age can be checked through the expected pension inquiry system of the Farmland Pension Integrated Portal (www.fbo.or.kr).
Lower and upper values are the values of 95% certainty on the probability distribution of the value generated by Monte Carlo simulation analysis of 30,000 trials.
As can be seen in the analysis results in <Table 4>, as a result of the Monte Carlo simulation analysis considering the stochastic process of the main variables applied to the basic actuarial model, we can see that the median of the probability distribution of shows all negative (−) values regardless of age group. This indicates that net profit will be generated for the guarantor through the operation of the farmland pension. Assuming that the farmland price is 100 million KRW, it shows us that the guarantor can get 4.73 million KRW if a farmland owner’s age is 60, 2.51 million KRW if a farmland owner’s age is 70, and 790,000 KRW if a farmland owner’s age is 80 based on the present value at time t=0, respectively.
In the case of farmland pension, the probability of the guarantor’s net loss that is, the probability that the net liability has a value larger than zero (Prob. ) appeared zero.4) In order to say that the farmland pension is actuarially fair, the amount of monthly payment (pmt) at which Prob. will have to be paid. If Prob. , we can say that the guarantor’s probability of net loss and net profit are each equal to 50%. The level of the monthly payment at which Prob. , which is the fair price, can be obtained through an optimization process. The optimization process is to repeatedly perform Monte Carlo simulation analysis of the same 10,000 trials until finding the level of monthly payment (fair price) that makes the median of the probability distribution became zero. The fair price of the farmland pension found in this study is shown in <Table 5>.
| Age | pmt: ① | Fair price: ② | Ratio: ②/① | Expected interest rate(i) |
|---|---|---|---|---|
| 60 | 311,090 | 357,359 | 1.148 | 2.91% |
| 70 | 388,290 | 435,525 | 1.121 | 2.82% |
| 80 | 518,080 | 558,134 | 1.077 | 2.87% |
As can be seen in <Table 5>, to become a fair price, compared to the current monthly payment, we can see that the amount must be increased by 14.8% for a 60-year-old, 12.1% for a 70-year-old, and 7.7% for an 80-year-old. Under the assumption that all other conditions in the basic actuarial model of farmland pension are the same (i.e., g=2.85% and the 2016 life table are applied), the expected interest rate in <Table 5> shows the level of interest rate that could be balanced with the 2% of actual fixed loan rate when the monthly payment at the fair price is paid. It can be seen that it is necessary to adjust the level of the expected interest rate applied to the basic actuarial model downward compared to the current level (i=3.65%) if the farmland pension intends to pay a fair price in the future.
This study evaluated the expected rate of return when the monthly payment in the current farmland pension is paid, and also evaluated the expected rate of return when the fair price was paid, and compared the size of both. Since the farmland pension is a product to which a non-recourse option is applied, the pensioner’s debt is limited within the farmland price even if the loan balance in the future time t becomes larger than the farmland price. Therefore, the expected rate of return on farmland pension is expected to vary greatly in the pattern before and after the crossover point where the size of the loan balance and farmland price intersect.
The evaluation point (N) of the expected rate of return in this study is 5-time points: ① N = 24 months, ② 120 months, ③ life expectancy, ④ 1.4 times the life expectancy, and ⑤ reaching the maximum life span (assumed to be 111 years old).5) After basically evaluating the change in the expected rate of return over time, we will additionally evaluate the expected rate of return at the crossover point to confirm the pattern before and after the point of intersection.
The crossover point is the point at which the value obtained by subtracting the farmland price from the loan balance changes from a negative (−) value to a positive (+) value. In this study, after generating a probability distribution of values through Monte Carlo simulation analysis, as we can see in <Table 6>, we found the point at which the median of the probability distribution changes from negative (−) to positive (+).
Note: (Bt−Lt) represents the median value of the probability distribution
As can be seen in <Table 7>, it can be seen that the crossover point arrives relatively faster when the fair price is paid compared to when the current monthly payment is paid. The evaluation point (N) of the expected rate of return by age, including the crossover point, is as follows.
An optimization process is also required to evaluate the expected rate of return at each evaluation point (N), which is to find the rate of return (y) that makes the median of the probability distribution of DN to be zero.
The expected rate of return for each evaluation point found through the optimization process is shown in <Table 8>.
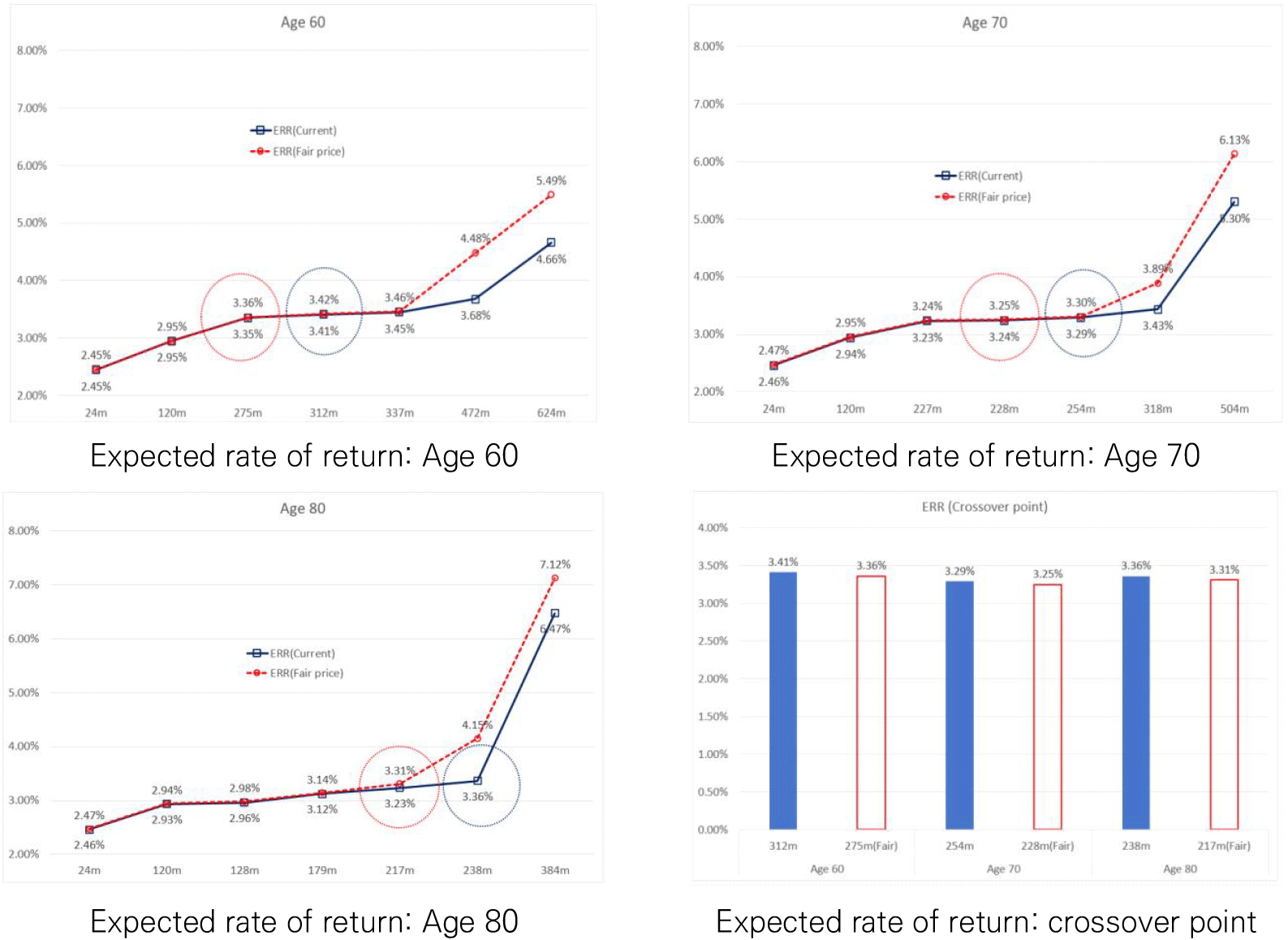
Looking at the results of the expected rate of return analysis, the size of the expected rate of return increases over time, showing a slower rate of increase until the crossover point is reached and then relatively faster after the crossover point. In addition, the values at the initial point did not show a significant difference between the case where the current pension amount was paid and the case where the fair price was paid, but it could be confirmed that the difference increased as time passed. By age group, the expected rate of return at the same time point (N) increases as the age group is relatively older. Although there is no significant difference in the size of the rate of return up to the crossover point for each age, we can see that the rate of increase of the relatively older age group after the crossover point is faster. <Figure 5> is a graphical representation of the expected rate of returns over time on the same plane for visual comparison.
As can be seen in <Figure 5>, when the fair price is paid as a monthly payment, the crossover point arrives a little faster than the current system, but the size of the expected rate of return at the crossover point did not show a significant difference between them. Therefore, the speed at which the expected rate of return increases after the crossover point becomes faster, so if the fair price is paid as a monthly payment, the size of the expected rate of return will not only increase compared to the current system but also the speed of increase in the expected rate of return would be relatively faster after the crossover point.
Assuming that a farmland pensioner leases farmland, the expected rate of return on rent for each evaluation point (N) can be obtained by calculating the geometric mean rate of return on rental rate of return. At this time, the expected rate of return on rent at a specific point in the future (N) can be evaluated using the median of the probability distribution after generating a probability distribution of the geometric mean rate of return on rent through Monte Carlo simulation analysis. The expected rate of return on rent for each evaluation point (N) is shown in <Table 9>.
Note: We reported the median values of the probability distribution of the expected rate of return.
As shown in <Table 9>, the yield curve of rent evaluated in this study was analyzed to have a very gentle downward-sloping shape. If the rental income effect that can be obtained by owning farmland is included, the expected rate of return realized by farmland pensioners could result in a 0.32%p to 0.36%p higher increase by each time point.
Ma (2022) has evaluated the expected rate of return of housing pension as shown in <Table 10>. When comparing the rate of return of farmland pension with that of housing pension, excluding the effect of rental income, the yield of farmland pension is higher than that of housing pension. While the housing pension charges 1.5% of the housing price as an initial guarantee premium, the farmland pension does not charge an initial guarantee premium. Due to the difference in the structure of the guarantee premium, the housing pension shows a very large negative (−) expected rate of return in the early stage, whereas the farmland pension shows a high positive (+) expected return of more than 2.45% in the early stage because it does not charge an initial guarantee premium.
Note: Refer to Ma (2022)
When the rental income effect is included, the homeowner’s expected rate of return on rent is significantly higher than that of the farmland owner, excluding the period where the initial negative rate of return occurs. As a result, the total expected rate of return of the housing pension is evaluated higher than that of the farmland pension.
Because housing pensioners have homeownership during the loan period, they do not need to pay rental costs. So, we can say that housing pensioners, although invisible, create the same amount of income as rental costs by using housing pensions. However, the rental income evaluated here is not the direct cash income of the housing pensioner, it is the invisible income. On the other hand, there is a difference between the two in that the rental income of the farmland owner is the cash income directly obtained by the farmland pensioner. Therefore, unlike the size of the expected rate of return evaluated, the cash income to be obtained by the housing pensioner is smaller than that of the farmland pensioner due to the monthly rent effect. So, in a situation where the level of monthly payment of the housing pension is lower than that of the farmland pension, the actual difference in cash amount between them will become slightly larger.
V. Conclusion
In farmland pension, for the convenience of calculation, it assumes a fixed average value of the main variables when determining the level of monthly payment using the basic actuarial model. Therefore, because the realized values could deviate greatly from the assumed values of main variables in the basic actuarial model considering that farmland pension is a long-term financial product, even if the equilibrium condition is satisfied in the basic actuarial model, the actual equilibrium condition may not be satisfied in the real world.
In this study, we want to check if the condition of equivalence (PVEL=PVEW) will be satisfied when the monthly pension amount determined by the current basic actuarial model is paid for life, by evaluating the stochastic process of main variables applied to the basic actuarial model of farmland pension. If the condition of equivalence is not satisfied, we want to check the level of fair price that can satisfy the condition when evaluated through realistic analysis considering the stochastic process of main variables. According to the analysis results of this study, if the monthly payment determined by the current actuarial model is paid for life, it was confirmed that the probability of loss suffered by the guarantor of farmland pension was zero. Assuming that the farmland price was 100 million KRW, it showed us that the guarantor could get 4.73 million KRW if a farmland owner’s age was 60, 2.51 million KRW if a farmland owner’s age was 70, and 790,000 KRW if a farmland owner’s age was 80 based on the present value at time t=0, respectively. The level of the monthly payment at which Prob. , which is the fair price, can be obtained through an optimization process. To become a fair price, compared to the current monthly payment, we could see that the amount must be increased by 14.8% for a 60-year-old, 12.1% for a 70-year-old, and 7.7% for an 80-year-old.
Subsequently, this study intends to evaluate the expected rate of return of farmland pensioners and evaluates the expected rate of return separately in the case where the monthly payment determined by the current basic actuarial model is paid and, in the case, where the fair price is paid. The size of the expected rate of return increases as time goes on. More concretely, while showing a slower speed of increase until reaching the crossover point, but after the crossover point showing a pattern of increasing at a relatively faster speed. And the values at the initial time points did not show a significant difference between the case where the current monthly payment was paid and the case where the fair price was paid, but it was confirmed that the difference increased as time passed. By age group, it was confirmed that the speed of increase in the relatively older age group increased faster after the crossover point. This study additionally evaluated the farmland owner’s rental rate of return. When we considered the rental income effect, it was confirmed that the expected rate of return realized by farmland pensioners could be 0.32%p to 0.36%p higher at each time point.
The fair price of farmland pensions presented through the analysis of this study could help farmland pension providers improve their products in the future. The expected rate of return evaluated and presented in this study is an evaluation indicator that is attempted for the first time about farmland pension and makes it possible to compare farmland pension with other pension products (e.g., immediate annuity). So, it is expected that it can be a useful indicator that can help consumers determine the final choice of product.