I. 서론
다세대주택은 중산층과 서민 계층의 주거 수요를 충족하는 주요 주거 형태로 자리하고 있다. 다세대주택은 아파트 다음으로 주택 수에서 상당한 비율을 차지하고 있다. 2015년 대비 2023년까지 서울시 인구 중 다세대주택 거주 비율은 23.4%에서 26.6%로 상승하였으며 주택 수 또한 같은 기간 28.2% 증가하였다(통계청, 2025). 주거비 부담이 큰 도시지역에서 다세대주택은 중산층 및 서민층의 실질적인 주거대안으로 기능하고 있어, 도시계획과 주거 복지의 측면에서 체계적인 관리와 정책적 지원이 요구된다.
다세대 주택은 아파트에 비해 개별성이 매우 큰 주택 유형으로 하위시장 내 가격의 이질성이 뚜렷하게 나타난다. 이는 다세대 주택이 아파트처럼 대규모 단지 형태로 기획 개발되지 않고 주로 소규모 필지 단위에서 민간 주도하에 개별적으로 건축되기 때문이다. 예컨대 동일한 블록 또는 읍면동 내에 위치한 다세대 주택이라 하더라도, 건축 시기, 시공사, 자재 수준, 접근성 및 주차시설 등에서 큰 차이가 발생하여 높은 개별성을 지니게 된다.
이러한 높은 개별성으로 인해 다세대주택 시장에서는 다세대 주택의 가격 형성이 불투명해지는 필연적인 문제가 발생하게 된다. 다세대주택은 동일주택에 대한 반복 거래 빈도가 낮고 인근 지역의 주택이 존재하더라도 비교사례를 찾기 어려워 개별 건물 수준 및 세대 수준의 정보 접근성이 낮다는 특성을 지닌다. 거래가 이루어지지 않는 기간에서 시장 가치를 객관적으로 파악하기 어렵게 되어 시장 참여자들은 가치 판단을 위해 추가적인 정보 탐색을 수행하게 되고, 이 과정에서 상당한 정보비용이 발생하게 된다.
이러한 낮은 거래 빈도와 시세 파악의 어려움으로 인해, 부동산 금융사고 발생 위험이 상대적으로 높다는 점이 문제로 지적된다(권경선, 2023). 특히 최근 다가구․다세대주택 등 저층주거지역 중심으로 임대인이나 건축주 등이 세입자로부터 전세보증금을 가로채는 대규모 전세사기 사건이 발생하면서, 사회초년생 및 서민 가정을 중심으로 주거 안정성이 훼손되고 금융기반이 악화하였으며, 나아가 사회 전반의 신뢰 수준이 저하되었다(황세은․장희순, 2023). 반복적인 사기 사건으로 인해 사회적 신뢰가 저하되면 결과적으로 불확실성의 증대로 인한 거주 안정성 악화와 사회적 비용이 증가하게 되는 악순환이 계속될 수밖에 없다.
이러한 정보 비대칭성을 해소하고 거주 안정성을 강화하는 방안으로 다세대 주택이 밀집한 지역의 세분화된 소지역 단위의 가격수준과 동향을 파악할 수 있도록 가격 지수 산정이 요구된다. 그러나 주택가격지수에 대한 선행 연구는 대부분 거래빈도가 높고 상품이 표준화되어 있는 수도권 지역의 아파트를 중심으로 하여, 다세대주택 시장의 소규모 지역에 대한 지수 작성에 관한 연구는 저조한 실정이다. 또한 다세대주택의 반복 거래가 드물고, 주택별 속성 정보도 미비한 경우가 많아, 전통적인 지수 작성 모형인 반복매매모형 또는 헤도닉 모형의 적용이 어렵다는 한계가 존재한다.
이에 본 연구는 국내 아파트 시장을 중심으로 검증되어 온 머신러닝 기반 자동평가모형(automated valuation model, 이하 AVM)을 다세대주택에 적용하여 반복거래가 적고 이질성이 큰 다세대 시장에서도 소지역 단위의 가격 수준을 안정적으로 추정할 수 있는지를 실증적으로 검토하고자 한다. 이를 위해 다세대 주택의 시점별 개별 가격을 추정하고 해당 추정가격을 기반으로 다양한 공간 단위의 가격지수를 작성하여, 한국부동산원에서 작성․발표되는 실거래가 매매지수, 주택가격동향조사 및 KB국민은행 주택동향조사 연립․다세대주택 매매가격지수 등 타 기관 작성 지수와 비교한다. 연구의 자료로는 2006년부터 2024년 12월까지 국토교통부에서 공개하고 있는 실거래가격과 과세산정의 기반이 되는 공동주택 가격정보 및 공간정보를 병합․활용하여 자동가치산정 모형을 산정한다.
부동산의 고가성과 시장의 이질성을 고려할 때, 시장 참여자에게 균등한 정보를 제공하고 안정적인 주거 서비스를 보장하기 위해서는 다세대주택 시장에서 소지역 단위 가격지수가 필수적이다. 이는 나아가 적정 가격 식별을 통한 깡통전세 방지, 임대차 안정성 판단등 임대차 보호의 영역뿐만 아니라 소지역별 수급 불균형 파악, 재개발․재건축 사업성 분석, 그리고 주택 공급 정책과 관련된 공공 개입의 기초자료로서 중요한 역할을 할 수 있다.
본 논문은 다음과 같은 구성으로 이루어져 있다. 제2장에서는 이론적 배경과 선행연구를 검토하고, 제3장에서는 학습을 위한 자료 구축 및 자동가치산정모형의 학습을 통해 개별 주택의 가격을 추정하고 이를 바탕으로 지수를 작성한다. 또한, 지수 작성 결과를 타 기관 작성 지수와 비교하는 과정을 다룬다. 마지막으로 제4장에서는 연구의 한계와 향후 연구 방향을 제시한다.
II. 이론적 배경 및 선행연구 검토
다세대주택은 「건축법 시행령」 별표 1(2025.1.21. 시행; 국토교통부, 2024)에 따라 연면적이 660제곱미터 이하이고 층수가 4개 층 이하인 주택으로 정의되며, 건축법상 공동주택의 한 유형에 포함된다. 법제화는 1984년에 처음 이루어졌으며, 이후 도시형생활주택 제도의 도입과 더불어 원룸형, 단지형, 복층형 등 도심 수요에 대응한 다양한 형태로 제도화가 확장되어 왔다.
실제 거래 및 통계 작성 과정에서 다세대주택은 물리적 외형이 유사한 다가구주택과 함께 ‘빌라’라는 용어로 혼용되기도 한다. 그러나 두 유형은 법적․제도적으로 뚜렷한 차이를 가진다. 특히 다가구주택은 하나의 건축물 안에 여러 세대가 거주할 수 있으나, 건물 전체가 하나의 소유권 단위로 간주되어 세대별로 개별 등기가 불가능하다. 반면, 다세대주택은 각 세대가 구분등기되는 구조로, 매매와 금융 활용에 있어 독립적인 거래 단위로 기능한다는 점에서 실질적인 차별성을 지닌다.
다세대주택은 1970년대 이후 최근 60년간 경제여건, 법제도 변화, 정부의 주거정책 기조에 따라 뚜렷한 공급 변화 양상을 보여왔다. 연도별로 살펴보면, 1986년, 1991년, 2002년에 다세대주택 신축 연면적이 큰 폭으로 증가한 것으로 나타난다. 1986년과 1991년의 주택 증가는 제도적 정비에 따른 새로운 주택유형의 도입과 주거 수요의 급증에 기인하며, 2002년의 급증은 IMF 외환위기 이후 경기부양을 위한 주택 경기 활성화 정책의 일환으로 해석된다(손병남 외, 2005, 장명준․강창덕, 2014).
최근 60년간 다세대주택은 일정 시기에 집중적으로 공급되어 이들의 물리적 노후화가 일정 임계점에 도달하면서 정비사업과의 연계가 강화되는 경향을 보이고 있다. 특히, 2000년대 이후 도시 중심부 및 1기 신도시 지역을 중심으로 다세대 및 다가구주택 밀집지역의 정비사업 추진이 본격화되며, 초기 공급된 다세대주택과 연립주택은 대개 20~30년 경과 이후부터 재건축대상이 되어 지역 부동산 시장에 가격 변동성과 재편 현상을 초래하는 요인으로 작용하고 있다.
한편, 다세대 주택 매매 시장은 금리환경 및 아파트 시장의 영향을 받아 거래량이 민감하게 반응한다. 2021년 이후 급격한 거래 위축은 다세대 주택에 대한 수요 불안정성과 투자 기피 현상을 보여준다. 한국부동산원이 집계․발표하는 ‘주택유형별 매매거래 현황(2021)’에 따르면 저금리와 유동성 증가로 인하여 거래량이 가장 많았던 2021년에는 다세대 주택의 매매 거래량이 전체 매매 거래량의 46.34%를 차지하여 아파트 매매거래량(38.76%) 보다도 높은 비중을 차지하였으나 부동산 시장이 본격적으로 냉각되기 시작한 2023년에는 다세대주택 매매 거래량은 33.82%, 2024년에는 29.58%까지 감소하였다. 이는 역전세와 전세전세로 인하여 수요가 급감하고 아파트로 매매가 쏠리는 현상이 심화하였음을 보여준다.
다세대주택은 아파트 단지보다 세대 수가 적어 동일 주택의 거래 빈도가 낮고 실거래 사례가 부족하기 때문에 시장가격의 불투명성이 필연적으로 발생하게 된다. 또한 다세대주택은 소득계층, 지역개발 수준, 도시정비 사업의 시행 여부와 방식, 진행 속도에 따라 공간적으로 뚜렷한 분포 특성을 보인다. 도시지역에서 사회적으로 중요한 역할을 하는 주거 유형인 만큼 다세대주택 시장을 체계적으로 판단하고 관리하기 위해서는 이러한 특성을 정확하게 포착하는 소지역 단위의 지수개발이 필수적이다.
주택 가격지수는 정부의 정책 수립, 수요자와 공급자의 시장 판단, 금융 대출자의 대출 여부를 판단함에 있어 중요한 정보가 된다. 주택 매매가격 지수를 산정하기 위해 가장 대표적으로 활용되는 모형은 헤도닉 가격모형(Hedonic regression model)과 반복매매모형(repeat sales model)이 있다.
먼저 헤도닉 가격모형 기반 지수는 주택 가격을 예측하기 위해 거래가격 또는 로그형태로 변환된 거래가격을 주택의 물리적 특성, 근린 특성 등의 변수에 회귀시키는 방식을 사용한다. 일반적으로 주택가격 결정에 영향을 미치는 요인에 관한 연구에서 연식, 면적과 같은 주택의 자체의 물리적 특성뿐만 아니라, 입지와 접근성, 시장 상황 등에 대한 변수들이 주택가격을 설명하기 위해 주로 활용된다(Chau and Chin, 2002; Freeman, 1979; Goodman, 1989; Goodman and Thibodeau, 1997; Ridker and Henning, 1967). 주택가격 결정에 영향을 미치는 주택의 내부 요인으로는 전용면적 층수, 향, 방의 개수, 화장실의 개수, 주차가능 여부 및 주차대수, 준공연도 및 리모델링 여부 등이 일반적으로 활용되어 왔다(Chau and Chin, 2002). 주택이 속한 단지 특성으로는 대지면적, 용적률, 입주연도, 시공사 또는 브랜드, 용도지역, 커뮤니티 시설 여부, 대지지분(조창섭 외, 2008) 등의 변수가 활용되었다.
헤도닉 모형 기반 지수는 두 가지 주요한 한계가 있다. 먼저, 헤도닉 모형의 선형성 가정이 주택시장의 변수를 파악하는데 비현실적이라는 점이다. 또한 거래가격에 영향을 미칠 수 있는 중요한 변수를 누락함에 따른 편향의 가능성이 존재하며 관측 기간 동안 모든 관측 주택을 대상으로 데이터의 지속적인 수집이 요구되므로 품질 유지가 어려운 점이 있다.
누락된 변수의 설명변수 문제에서 자유로운 반복매매 모형은 동일한 주택이 재판매되는 경우, 해당 주택이 두 거래 간에 변하지 않았다는 전제 하에 가격 변화를 관측할 수 있다(Bailey et al., 1963; Case and Shiller, 1987). 그러나 해당 방식 역시 거래가 부족한 시장 변동기 또는 하위시장에 대한 지수를 산정할 때 사용 가능한 거래데이터가 줄어들어 필연적으로 안정적인 주택지수를 산정하는 것이 어렵게 된다는 한계가 있다. 또한 실제로 동일한 주택이 두 거래 시점 사이에 변하지 않았는지 확인하는 것 역시 현실적으로 어렵다는 점이 한계로 지적된다.
이러한 한계를 보완하고자 두 접근법의 장점을 결합한 하이브리드 모형 등이 제시되었으며, 최근에는 머신러닝 기법이 발전하면서 기존의 헤도닉 모형을 대체하거나 보완하는 방식으로 널리 활용되고 있다(Hjort et al, 2022).
국내 다세대주택 가격지수로는 조사․평가기반 가격에 기반한 한국부동산원에서 제공하는 주택가격동향조사 내 다세대 연립지수, KB국민은행에서 제공하는 주택가격동향조사 내 연립 다세대 가격지수가 있다. 또한 한국부동산원은 실거래가격에 기반한 공동주택 실거래가격지수를 2006년 1월부터 월별로 제공하고 있다. 세 가지 지수 모두 반복매매모형을 적용하여 산정한 지수로서, 가격 작성의 가장 작은 공간 단위는 서울시로, 서울시 내부의 하위 공간 단위별 지수는 작성되고 있지 않다. 이는 반복매매 특성상 하위 지역에 대한 지수를 작성할 경우 표본이 감소하여 안정적인 지수 작성이 어렵다는 점에서 기인한다.
소지역이란 동일 소지역 내에서는 동일한 사회적․경제적․행정적 특성을 공유하여 다른 지역과는 구분되는 지리학적 지역을 지칭한다. 예를 들어 소득 수준이 유사한 읍․면․동이나 같은 행정 제도의 영향 아래 있는 시․군․구 등이 이에 해당한다(우남교․권범준, 2016). 이러한 동일 소지역 내에서 부동산은 가격 변화의 측면에서 유사한 속성을 나타내는 경향이 있다(이석준, 2019).
최근 부동산 시장에서는 과거보다 소지역 단위에서의 가격 동향의 차이가 두드러지게 나타나고 있으며, 이는 정책 수립과 시장 파악에 어려움을 초래하는 요인 중 하나로 제시된다(우남교․권범준, 2016).
소규모 지역을 대상으로 가격지수를 작성한 대다수의 국내 연구는 아파트를 대상으로 하며 작성되는 지수의 공간적 단위도 생활권 단위(김이환 외, 2022), 시군구 단위(구본일․김재익, 2016) 또는 2기 신도시 지역(송의현․김경민, 2019) 단위의 연구들이 대부분이다. 해외의 경우 인구조사구 단위(Francke et al., 2023), 500×500m 육각형 단위의 소지역 단위(Ahlfeldt et al., 2023)에서의 가격지수 작성이 시도되었다.
소지역 단위 가격지수를 산정함에 있어서 전통적 회귀에 기반한 모형으로, 지역가중 회귀, 공간 동적 요인 모델, 베이지안 추론방법을 활용한 연구들이 존재한다. 먼저 Ahlfeldt et al.(2023)은 반복 횡단면 패널 데이터를 활용하여 지역 가중 회귀(locally weighted regressions, 이하 LWR) 기법을 활용하였다. 해당 연구에서 산정된 지수는 하위 시장 경계를 넘어 발생하는 공간적 불연속적 변동을 반영할 수 있도록 하였으며 500×500m 육각형을 단위의 주택가격지수와 임대료가격지수를 작성하였다.
Francke et al.(2023)은 공간 동적요인모델(spatial dynamic factor model)의 적용을 통하여 인구조사구(census tract) 수준의 분기별 지수를 구축하였다. 데이터가 부족한 지역에 대하여 인근 유사 시장으로부터의 정보를 포착하여 잠재 추세에 대한 부하가 공간적 임의 보행을 따르도록 하였다. 이로 인하여 생성된 지수는 비공간적 모형으로 구축된 유사한 지수보다 잡음이 적으며, 반복매매쌍이 충분히 존재하는 지역에서는 전통적인 반복매매모형으로부터 얻은 지수와 유사한 결과를 보이고 있음을 보고하였다.
우남교․권범준(2016)은 베이지안 추론 방법을 활용하여 시군구 단위의 주택매매가격지수를 추정하는 방법을 제시하였다. Fay-Herriot 모형을 기반으로 계층적 베이지안 추론을 적용하고 깁스 표집기를 사용하여 추정값의 정도를 비교하였다. 이를 통해 향후 읍면동별 지가 지수의 소지역 모델링을 통한 다양한 부동산 가격 지수들의 추정이 가능함을 제시하였다.
최근 아파트 단지 단위로 머신러닝 가격을 추정한 후 이를 다양한 상위 공간 단위로 지수화하는 연구들이 진행되었다(김진석, 2024; 이소영․김경민, 2025).
김진석(2024)은 아파트 단지 단위에 대하여 아파트 매매가격지수를 산정하였으며 본 연구에서 제안하는 머신러닝 기반 가격지수는 기존에 발표 되고 있는 평가 기반 지수에서 발생하는 평활화 문제를 해소하여 주택시장의 흐름을 더 정확하게 반영하면서, 시간 더미 지수보다는 안정적이고 소지역을 대상으로 분석할 수 있다는 장점이 있음을 제시하였다. 더 나아가 기존 선행연구에서는 어려웠던 소지역 대상 부동산 정책이 주택가격 흐름에 미친 영향을 분석하였다. 구체적으로는 서울 27개 동에 적용된 민간택지 분양가 상한제가 아파트 가격지수 상승률에 미친 영향을 행정동별로 분석하였으며, 이중차분모형을 통해 분양가 상한제가 유의미하게 아파트 가격 상승에 부정적인 영향을 미쳤다는 정책 효과를 구체적으로 규명하였다.
이소영․김경민(2025)은 LightGBM과 ANN모형으로 추정한 가격을 기반으로 개별 주택, 아파트 단지, 행정동, 시군구, 생활권별 월세지수를 산정하였다. 기계학습 추정가격에 기반한 가격지수는 실거래가기반의 반복매매 월세지수와 비교하였을 때 유사한 누적상승률을 보였으며, 거래가 없는 기간과 단지 및 읍면동, 시군구, 생활권 등의 세부 공간 단위에서 지수를 산정할 경우 표본손실이 발생하여 불안정한 지수가 산정되는 반복매매지수와 달리 시의성있고 안정적인 추정성능이 있음을 제시하였다.
해당 절에서는 머신러닝 모형을 활용하여 다세대주택 가격지수를 산정하기 위한 주택가격 추정 모형을 구축함에 앞서 다세대주택의 가격에 영향을 미치는 요인을 선행연구를 통해 검토하고 본 연구의 차별성을 제시한다.
기존 주택 가격에 영향을 미치는 요인들을 검토한 연구들은 주택 유형 중에서도 아파트를 중심으로 꾸준히 진행되어 왔는데, 국내 다세대주택만의 가격결정요인에 관한 연구는 도시 및 광역시 단위가 아닌 밀집지역 또는 몇 개의 동으로 한정되어 있어 일반화가 어려운 점이 제시되었다(김남현․오세준, 2017; 송선주․황정수, 2015; 양승철, 2014). 이는 다세대 주택이 소득계층, 지역개발 수준, 도시정비 사업의 시행 여부와 방식, 진행 속도에 따라 공간적으로 뚜렷한 분포 특성과 이질성으로 인한 것으로 판단된다.
송선주․황정수(2015)의 연구에서는 다세대주택 가격에 영향을 미치는 요인들을 지역특성, 입지특성, 건물특성, 주호특성으로 분류하여 헤도닉 모형의 다중회귀분석을 실시하였다. 분석 결과, 주변 아파트의 시세가 다세대주택 매매가격에 상당한 영향을 미치며, 대상 주택이 소재한 지역의 경사도, 건물의 향도 유의하게 영향이 있는 것으로 나타났다. 또한 직전연도의 다세대주택 공급량이 적을수록 당해 매매가격이 상승하는 것으로 제시하였다.
김진명․이춘원(2023)은 재개발구역의 연립주택 및 다세대주택의 가격 결정요인으로 건물 전용면적, 공시지가, 대지권 면적, 건물 경과연수, 도로접면이 주택 가격에 미치는 영향을 분석하였다. 분석 결과, 경과연수와 대지권 면적, 건물의 전용면적, 공시지가가 실거래금액에 정의 영향을 미치고, 건물의 경과연수는 실거래 금액에 부의 영향을, 도로접면은 실거래금액에 유의미한 통계적 영향을 미치지 않았다고 보고하였다.
이수정․노승한(2025)은 서울시 소규모주택정비 관리지역인 모아타운에 소재한 다세대 연립주택 6,061건의 매매가격을 분석하였다. 종속변수인 단위면적당 거래가격에 대하여 관리지역 면적, 노후 불량 건축물 비율과 같은 사업 구역 특성, 대지권 면적 및 층수와 같은 토지 건축물 특성, 초등학교․응급의료기관 등 주요 시설까지의 거리와 같은 입지 특성을 독립변수로 구성하였다. 거래 시기 효과 측면에서는 2018년 이후 가격 상승폭이 확대되며 2021년과 2022년에 특히 가격이 급등하였다고 제시하였다.
본 연구는 그동안 상대적으로 연구가 미흡했던 다세대주택을 대상으로 고해상도 주택가격지수를 산정한다는 점에서 기존 연구와의 차별성을 지닌다. 특히 방법론적 측면에서, 아파트 가격 추정 분야에서 안정성과 효율성이 입증된 머신러닝 방법을 이질성이 높은 다세대주택 가격 추정에의 적용 가능성을 검토한다. 이를 위해, 아파트 가격 산정 모형에서 주로 활용된 변수들과 함께, 기존 선행연구를 통해 파악된 경사도, 건물의 향, 블록 단위의 근린 특성 등 다세대주택의 개별성에 기여하는 요인들을 반영한다. 이러한 고해상도 지수는 지역별 가격 수준과 가격 변동 추이를 세밀하게 파악할 수 있어 향후 거래량, 토지이용계획 및 용도지역 변경, 가로주택정비사업, 공공재개발 등의 정비사업 정책, 정책적 연계성과 관련된 논의로 확장하고자 한다.
III. 가격지수 산정
다세대주택 매매가격지수 산정의 대상이 되는 주택 자료로는 과세 목적으로 공개되는 공동주택가격정보 및 공동주택가격공간정보를 활용한다. 해당 자료는 서울 지역에 소재한 다세대주택 건물동을 구성하는 개별 세대의 층, 호 그리고 전용면적 정보를 제공하며, 지번 주소 또는 도로명 주소와의 매칭을 통해 실거래가격과 병합할 수 있다. 병합에 사용한 자료는 <표 1>과 같다.
| 변수명 | 공동주택 가격공간정보 | 공동주택 가격정보 | 국토교통부 실거래가격 | 예시 |
|---|---|---|---|---|
| 법정동 | O | O | O | 서울시 은평구 수색동 |
| 지번 | O | O | O | 12-34 |
| 공동주택명 | O | O | O | @@맨숀 |
| X좌표 | O | 126.9057 | ||
| Y좌표 | O | 37.6051 | ||
| 산정공동 주택호수 | O | 8세대 | ||
| 동명 | O | A동 | ||
| 층명 | O | 3 | ||
| 호명 | O | 301 | ||
| 전용면적 | O | O | 45.51m2 | |
| 매매가격 | O | 35,000(만원) |
주: 원데이터의 좌표계는 EPSG 5171이나 예시를 위하여 EPSG 4326으로 변환함.
또한 본 연구에서는 근린환경 및 블록에 대한 정보를 ‘기초구역’으로 반영한다. 기초구역이란 우편번호 통계, 소방, 우편 등의 목적으로 국토를 일정한 단위로 구분한 공간 경계단위이다. 2025년 4월 기준으로 총 5,666개의 기초구역이 존재하며, 그 중 다세대주택이 소재한 기초구역은 총 3,634개로 해당 구역의 중위 면적은 0.52km21) 이다.
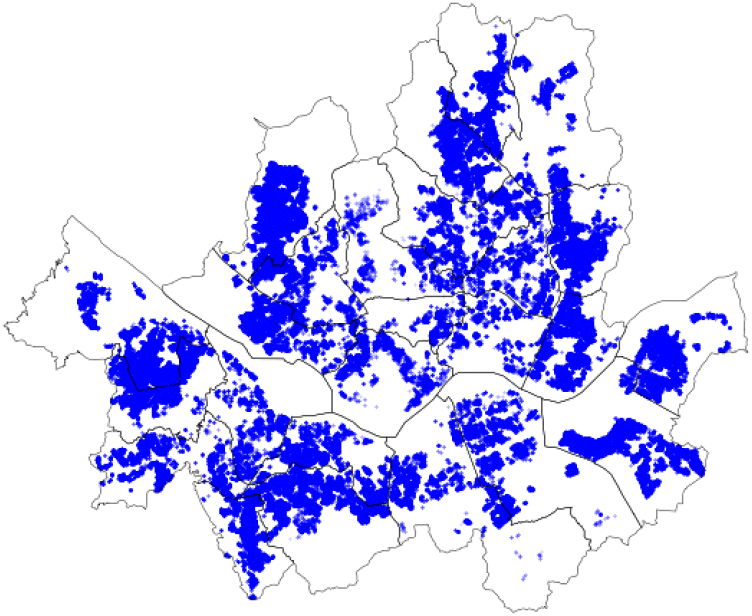
공동주택 가격정보를 통해 파악한 공시대상다세대주택은 총 90,800개 주택(총 838,681세대)으로, 1개 다세대주택 건물동 당 평균 세대수는 9.23세대로 파악되었다. 실거래가격과 병합하였을 때 주택의 주소지가 불분명함 등의 사유로 병합되지 않는 경우를 제외할 경우 총 71,970개 주택(총 657,793세대)으로 지수산정 대상이 되는 주택이 최종 확정된다. 각 다세대주택의 공간적 분포는 <그림 1>과 같으며, 구별 주택 집계수는 <표 2>와 같다. 은평구, 강서구, 송파구, 양천구, 강북구 순으로 주택 수가 많은 것으로 나타났다.
주: 전체 주택수는 657,793호로, 주택수 집계는 오름차순으로 정렬함.
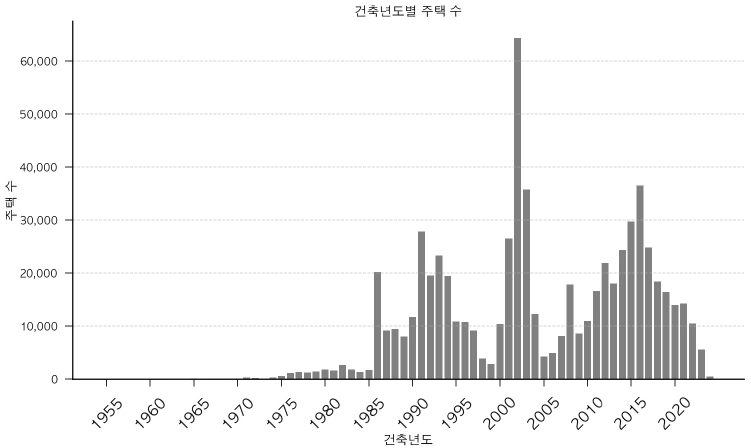
건축년도를 기준으로는 2001~2004년 사이에 신축된 주택의 빈도가 높은 것으로 파악되었다(<그림 2> 참조). 또한 1998년 금융위기 이전과 2008년 금융위기 이후에도 다세대주택의 공급이 지속적으로 증가하다가 2024년 최근 공급량이 감소한 것으로 나타났다. 이는 앞서 다룬 것처럼 1986년, 1991년, 2002년경 다세대주택 신축 연면적이 큰 폭으로 증가하였다고 제시한 선행연구와 동일하다.
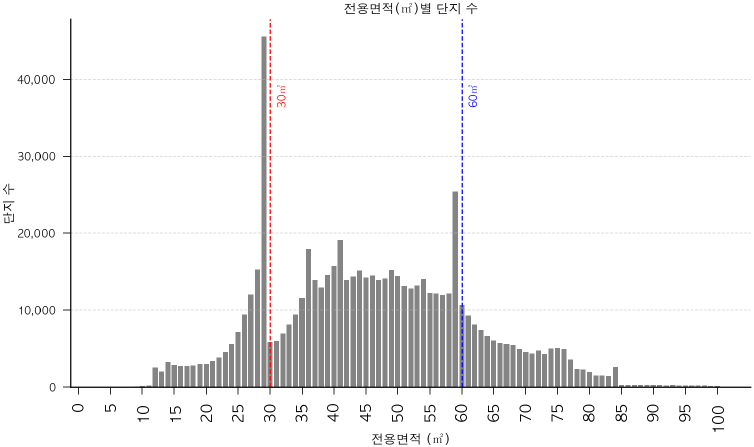
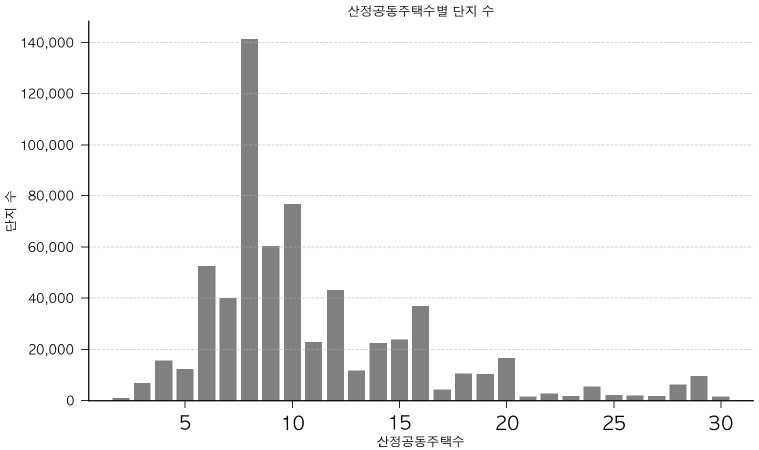
전용면적대 별로는 30m2 직전 이하 구간과 60m2 직전 구간의 빈도가 매우 높았으며, 이는 주차 설치기준에 따른 면적 구간을 초과하지 않으면서도 분양면적을 최대화하려는 공급 경향이 나타난 것으로 볼 수 있다(<그림 3> 참조). 세대수 기준으로는 8세대로 구성된 주택이 가장 빈도가 높은 것으로 나타났다(<그림 4> 참조).
실거래가는 국토교통부에서 제공하는 실거래가격 자료를 활용하였으며, 2006년부터 2024년 12월까지의 다세대․연립주택 데이터를 집계하였다. 지수 산정 대상 주택과 실거래가격을 매칭하는 과정에서 실거래가격 상 주택의 지번 또는 도로명 주소가 명확하지 않아 매칭이 불가능한 실거래건을 모형 훈련 대상에서 제외하였다. 그 결과, 전체 실거래가의 약 16.5%가 제외되었으며, 이 중에는 멸실된 주택으로 추정되는 사례나 연립주택으로 분류되어 다세대주택의 공시 대상 주택 목록에서 제외된 사례 등이 포함된 것으로 판단된다. 이에 따라 정제 전 총 798,392건의 거래 중 599,303건이 최종적으로 훈련 모형에 투입되었다.
서울 전체 및 생활권별 중위가격 및 평균가격 추이와 거래량은 <표 3>과 같다. 중위가격은 2006년 대비 2024년에 약 2.61배(30,000/11,500) 상승한 것으로 나타났으며, 평균가격은 약 2.65배(34,219/12,903) 상승한 것으로 파악되었다. 거래량은 2021년까지 4만 8천여 건을 기록하다가 급격한 시장 침체로 2023년 1만 8천여 건을 기록하고, 2024년 2만 2천 건으로 회복하였다.
기존 연구에는 주택 가격을 추정하기 위한 머신러닝 모형으로 서포트 벡터 머신(support vector machine), 인공신경망(artificial neural network), 장단기 메모리(long short-term memory) 모형, 랜덤 포레스트(random forest), 캣부스트 모형(CatBoost), 그래디언트 부스팅 모형(Gradient boosting model)이 주로 활용된다(김이환 외, 2022; 배성완․유정석, 2018a; 2018b; 이소영․김경민, 2025; 홍정의, 2021). 본 연구에서는 그래디언트 부스팅 모형(Gradient boosting model, 이하 GBM)의 일종으로서 속도와 효율성을 개선한 모델인 LightGBM(4.6.0 버전)을 활용하여 가격추정모형을 구축한다. LightGBM은 하위시장 식별, 단기적 시장 반응의 포착, 추정의 정확성 및 속도 측면에서 소규모 지역 단위의 지수 산정을 위한 가격 추정에 강점을 지닌다.
먼저 LightGBM은 트리 기반 모형으로서, 입지․규모․품질․입지에 따라 구별되는 하위시장의 유사한 특성을 찾아내고 설명력을 훼손하지 않으면서 하위시장의 평균 특성을 효과적으로 포착할 수 있으므로 소지역 단위의 지수 작성에 있어 유리한 장점으로 작용한다(홍정의, 2021; Fan et al., 2006). 특히 LightGBM은 다른 트리 기반 모형 중에서도 수준 단위 분할 방식(level-wise)으로 나무를 성장시키는 랜덤 포레스트와 캣부스트와는 달리, 손실 감소 효과가 큰 노드를 중심으로 나무를 성장시키는 리프 분할 방식(leaf-wise)을 채택하여 잔차 감소 폭이 크고 정밀한 분할이 가능하다는 점에서 개별성이 높은 다세대 주택에 대한 정밀한 추정이 가능할 것으로 판단되었다.
LightGBM이 기반하고 있는 트리기반 학습방식은 단기적 시장 반응을 포착할 수 있다. 이소영․김경민(2025)는 인공신경망 모형 추정 가격기반 지수가 연속적인 가중치 업데이트를 통해 출력이 부드럽게 변화함으로써 상당한 평활화 효과가 보인 것과 달리 LightGBM 추정 가격기반 지수는 시장의 단기적 변화를 민감하게 반영하는 형태를 보인다고 하였다.
마지막으로 정확도와 속도 측면에서 LightGBM의 장점이 있다. 과거 선행연구에서 아파트 가격을 추정함에 있어 대체로 평균절대오차(mean absolute percentage error, 이하 MAPE) 4.8%~3.8% 예측 성능이 우수한 것으로 보고되었다(김진석, 2024; 이소영․김경민, 2025). 모델의 속도 측면에서 공시가격 주택정보를 기준으로 아파트 단지 수(9,430개 단지)보다 약 7.4배 많은 다세대주택 단지 수(71,970개)에 대한 데이터 용량을 처리하는데 속도 측면에서 장점을 보인다. LightGBM은 범주형 변수를 One-hot 엔코딩 없이 직접 사용할 수 있다.2) 이러한 특성 덕분에 거래 시점과 같은 시점 정보 및 주택, 지역 또는 근린에 대한 정성적 정보를 정수화하여 투입할 수 있으며, 이러한 변수들은 일반적인 헤도닉 모형에서 더미 변수로 처리하여야 하지만, LightGBM은 이를 정수의 수열로 인식하고 처리하므로 연산의 효율성과 속도 측면에서 유리하다.
그래디언트 부스팅 모형이란 Friedman(2001)이 최초로 제안한 모형으로 결정트리를 순차적으로 학습시켜 예측 성능을 향상시키는 기계학습 모형이다. 모형의 오차를 최소화하는 방식으로 경사하강법(gradient descent) 활용하며, 예측력이 약한 여러개의 모형을 결합시키는 방식으로 강한 예측 모형을 구축하게 된다. 초기 Friedman(2001)이 제시한 그래디언트 부스팅 알고리즘은 다음과 같이 초기화 과정과 반복과정으로 구성된다.
(a) 초기화 과정(Initialization)
초기 예측 함수 fc를 다음과 같이 설정한다.
(b) 반복 과정(Iteration)
(b-1) 기울기 계산(Gradient Calculation)
현재의 예측 함수fc에서 손실함수 기울기(gradient) ∇ f를 계산한다.
(b-2) 기저 학습자 선택(Base Learner Selection)
기울기 ∇ f에 가장 근접한 기저학습자 g를 탐색한다.
(b-3) 이동 거리 계산(Line Search)
현재 함수 fc와 선택된 기저 학습자 g의 선형 조합에서 최적 이동 거리(step size) ρ를 계산한다.
(b-4) 모델 업데이트
계산된 방향과 이동거리를 반영하여 예측 함수를 업데이트 한다.
이와 같은 과정을 통하여 그래디언트 부스팅 모형은 각 단계에서 잔차를 효과적으로 보완함으로서 예측 정확도가 점진적으로 향상된다.
LightGBM은 그래디언트 부스팅의 일종으로 일반적인 트리 기반 모델에서 사용하는 레벨(level) 기반 분할 방식이 아닌, 리프(leaf) 중심 분할 방식을 채택한다. 레벨 기반 분할은 트리의 깊이를 일정하게 유지하면서 균형 있게 노드를 분할하지만, 리프 중심 분할은 손실 감소가 큰 리프를 우선적으로 분할함으로써 비대칭적인 트리 구조를 허용한다. 이러한 방식은 리프 내 데이터 수를 고려하면서도 손실 감소를 극대화하여, 예측 오차를 최소화하는 방식으로 학습이 가능하다.
본 연구에서는 다세대주택의 시점별 가격을 추정하기 위하여 훈련을 위한 타겟 변수(target variable)3) 로 주택가격(price)을 사용하였다. 학습 변수(feature variable)로는 해당 주택의 위도(lon)와 경도(lat), 전용면적(area), 거래 시점(trade_time), 주택 층수(floor), 해당 주택 건물동의 총 세대수(gencount), 인접 도로 유형(road_type), 준공연도(built_year), 해당 단지 고유번호(danji_index), 기초구역고유번호(base_id)를 우선적으로 투입하였다(<표 4> 참조).
주: 위도, 경도 좌표는 EPSG 5171 기준함.
또한 주택이 소재한 단지의 고유번호는 정수화(danji_index; 0~90,799)하여 투입되었다. LightGBM과 같은 트리 기반 모형에서는 정성 변수를 효율적으로 적용하기 위하여 비가측 범주형 데이터이면서 정수화된 데이터를 반영할 수 있다(홍정의, 2021). 이는 공개 데이터로는 파악하기 어려운 해당 다세대주택 단지의 주차대수, 리모델링 여부, 용적률, 시공사, 향, 경관, 승강기 설치 여부, 복도형태 등 개별 주택 단지가 가지고 있는 비가측적 요인들을 효율적으로 대리변수화 하는 효과를 갖게 된다.
이와 같은 맥락으로 근린 환경을 대리변수화한 기초구역 고유번호(base_id; 0~3,634)를 투입하였다. 해당 변수는 지역 내 다세대주택 단지들이 공유하는 근린 환경, 즉, 교육시설, 공원, 병원 등과 같은 시설까지의 접근성 및 지형, 지세와 같은 요소들을 효율적으로 대리변수화 할 수 있다. 이러한 입지 효과 변수의 투입 효율성은 투입 여부에 따른 모형의 성능의 비교를 통하 최종적으로 검토한다.
주택이 접하는 도로에 대한 변수(road_type)로는 각 주택의 도로명으로부터 파악하여 분류 불가한 경우를 기준으로 대로, 로, 길에 따라 0, 1, 2, 3로 분류하여 부여한 값을 투입하였다.
시간에 대한 정보로는 2006년 1월 기준으로 0부터 2024년 12월까지의 227로 끝나는 trade_time 변수를 투입한다. 이는 홍정의(2021)에서 제시한 것과 같이 주택가격 추정 모형이 거시경제 효과 자체를 묘사하는 모형이 아니라, 시점에 따라 달라진 변화를 데이터 기반으로 감지하기 때문에 명시적으로 거시환경 변화를 변수화할 필요가 없는 점을 고려한 것이다.
일반적인 시계열 자료를 활용하여 머신러닝 모형을 훈련하는 경우, 시간 선 후에 따른 순서를 고려하여 훈련 데이터와 테스트 데이터를 분할한다. 이는 모델이 온전히 학습변수만으로 가격의 상승 및 하락 추세, 정책 변화 등을 적절히 반영할 수 있도록 하기 위함이다. 만약 무작위 분할을 사용할 경우, 모형이 미래 시점의 정보를 학습하여 과거를 예측하는 편향(look-ahead bias)이 발생할 수 있으며, 이로 인해 예측 성능이 과대 평가 되는 결과가 초래될 수 있다.
본 연구에서는 다세대주택의 소지역 단위 가격지수를 산정하기 위해 머신러닝 모형을 적용함에 있어 무작위 분할 방식을 채택하였다. 다세대주택 시장의 특성상 거래가 이루어지지 않는 기간이 빈번하게 발생하고, 이로 인해 시점별 가격 정보에 결측이 존재하는 경우가 많다. 전통적인 반복매매지수나 헤도닉 가격지수 방식은 이러한 결측으로 인해 지수가 불안정해질 수 있지만, 머신러닝은 시계열 상 결측이 존재하는 시점의 가격을 추정할 수 있으며, 추정 가격을 기반으로 안정적인 지수 산정이 가능하다. 예컨대, 1월부터 3월까지 거래 가격이 관측되었으나 4월에는 거래가 없어 가격 정보가 존재하지 않고, 5월에 다시 거래가 이루어진 경우, 본 연구의 머신러닝 모형은 4월의 잠재 가격을 추정하기 위해 1~3월과 5월의 정보를 모두 활용할 수 있어야 한다. 이와 같이 결측 구간을 포함한 시계열 예측 상황에서는, 무작위 분할을 통해 모형이 시계열 전 구간의 다양한 시점을 학습하도록 하는 것이 보다 효율적이다.
또한, 지수 작성 과정의 특성상 특정 시점에서 산정하는 가격지수는 이미 경과한 과거 시점의 시장 상황을 반영하는 것이므로, 해당 시점 기준으로 과거의 모든 거래 정보를 확보하였다는 가정 하에 모형을 구성할 수 있다. 이러한 점을 종합하여 시계열 순서를 고정한 분할 방식보다 무작위 분할이 적합하다고 판단하였다.
주택가격은 이분산성(heteroskedasticity)을 지니는 것으로 알려져 왔다(Fleming and Nellis, 1984; Goodman and Thibodeau, 1997). 주택가격의 이분산성이란 주택가격을 설명하는 회귀모형에서 오차항의 분산이 일정하지 않은 현상을 말한다. 일반적인 회귀 회귀모형에서는 이러한 이분산성을 효과적으로 완화하기 위하여 종속변수를 로지스틱 변환하거나 동분산 가정이 완화된 일반화 최소제곱법(Generalised least squares)등을 적용할 수 있다. 그러나, 머신러닝을 통해 가격을 추정할 경우 비선형적 패턴 학습을 통해 일반적인 회귀모형에 비하여 이분산성의 영향을 크게 받지 않는 것으로 보고되었다(Gelfand, 2013; Munir, 2023).
머신러닝은 손실함수 설정을 통해 예측값과 실제값의 오차를 줄이는 방향으로 모형을 훈련하며, 일반적으로는 MSE(mean squared error)를 기본적으로 적용하여 예측한 값과 실제 관측한 값의 차이를 제곱하여 평균한 오차를 줄여나가게 된다. Hjort et al.(2022)는 머신러닝을 사용하는 목적에 따라 SE(squared error)와 SPE(squared percentage error) 두 가지 손실함수를 비교하여, 만약 전체 주택가치 총액에 대한 오차를 줄이기 위한 방향으로 손실함수를 설정할 경우 SE 손실함수가, 주택 개별 자산에 대한 오차를 줄일 경우 SPE 손실함수가 적절함을 제시하였다.
본 연구에서는 LightGBM 라이브러리에서 제공하는 다양한 손실함수를 통한 성능 비교 후 가장 성능이 우수한 모형을 지수산정에 채택하였다. 일반적으로 국토교통부 실거래가격을 통하여 머신러닝 가격추정모형을 구축한 기존 연구에서는 평균제곱오차(mean squared error, 이하 MSE)4) 를 활용하는 연구가 대다수를 차지하며 다양한 손실함수를 검토한 연구는 드물다. 평균제곱오차는 실제값과 추정값의 오차의 제곱값을 최소화하는 형태로 손실을 최소화한다. 이와 함께 고가 주택 구간에서의 오차의 과대 반영 가능성을 고려하여 오차의 절대 크기를 최소화하는 평균절대오차(mean absolute error, 이하 MAE),5) 저가주택의 분포를 반영하여 연속성과 이산성의 중간 성격을 가진 데이터에서 손실을 최소화하는 Tweedie Loss6) 등 세 가지 손실함수를 적용한 모형을 훈련 후 추정 성능을 비교하였다.
또한 최적의 하이퍼파라미터를 탐색하기 위하여 Optuna를 활용하여 총 50회의 실험을 수행하였으며, 각 실험은 최대 10,000회의 반복(iteration)으로 설정하였다. 이때, MAPE 값의 개선이 30회 연속으로 발생하지 않을 경우 조기 종료(early stopping) 기법을 적용하여 과도한 반복으로 인한 과적합을 방지하였다. 하이퍼파라미터 탐색 도중 검증 데이터셋의 MAPE 값이 약 10%에서 9% 수준까지 도달한 이후에는 추가적인 성능 개선이 관찰되지 않았으며, 이를 통해 모형의 일반화 성능이 확보되었음을 확인하였다. 이와 같은 탐색 과정에서 가장 우수한 추정 성능을 보이는 것으로 제시된 실험 결과(best trial)의 파라미터를 최종 하이퍼파라미터로 선정하였다(<표 5> 참조).
| Parameters | 탐색 범위 | 최적 설정 |
|---|---|---|
| learning rate | 0.01~0.3 | 0.027 |
| num_leaves | 16~1024 | 828 |
| max_depth | 3~16 | 14 |
| min_data_in_leaf | 5~50 | 8 |
| feature_fraction | 0.6~1.0 | 0.867 |
| bagging_fraction | 0.6~1.0 | 0.916 |
| bagging_freq | 1~7 | 4 |
모형의 성능을 확인할 수 있는 지표로 설명력 지표(R-sqaured)와 RMSE, MAE, MAPE를 활용하여 비교하였다. 비교 결과 가장 정확도가 높은 모형은 상호작용항이 없는 모형으로 Tweedie 손실함수를 적용한 모형을 최종적으로 선정하여 개별 주택의 가격을 추정하였다.
먼저 상호작용항이 있는 경우가 없는 경우보다 전반적으로 MAPE 값이 높게 도출되었는데, 이는 상호작용항을 추가할 경우 모형은 더 복잡한 상호의존성을 학습하게 되어 상호작용항이 예측력 향상에 기여하지 않고 오히려 불필요한 패턴을 학습하기 때문으로 해석할 수 있다(<표 6> 참조). 이러한 결과는 다세대주택이 소규모 필지에 개별적으로 개발되는 특성, 표준화되지 않은 구조, 세대 간 거래의 희소성 등의 요인으로 인해 면적과 층수와 같은 주요 변수 간 상호작용 효과가 일관되게 나타나지 않고, 지역 및 개별 주택의 특성에 따라 상호작용 효과가 국지적으로만 나타나고 전체적으로는 비일관적인 형태를 띠게 되어 예측 성능을 저하시킨 것으로 판단된다.
입지 변수를 포함함에 따라 모형의 예측 정확도가 향상되는지를 추가적으로 검토하였다. 홍정의(2021), Hjort et al.(2022), Kim and Kim(2023)은 위도와 경도만으로도 주요 시설까지의 접근성이나 행정구역 등 입지에 따른 비선형적인 가치 차이를 효과적으로 포착할 수 있음을 보였다. 본 연구에서는 다세대주택의 단지 특성과 근린 특성의 이질성을 반영하기 위하여, 단지 특성을 나타내는 단지 고유번호와 근린 특성을 나타내는 기초구역 고유번호를 변수로 추가하였다. 만약 이러한 변수들의 도입으로 모형의 예측 성능이 개선된다면, 이는 위도․경도와 같은 지리적 좌표를 통해 포착된 입지 정보만으로 설명되지 않는 단지 및 기초구역 단위의 미시적 입지 특성이 모형에 유의미하게 반영되었음을 의미한다.
입지 변수를 투입한 모형 간의 성능을 비교한 결과(<표 7> 참조), 경도와 위도뿐만 아니라 단지 ID 및 기초구역 ID를 모두 포함한 모형이 가장 우수한 예측력을 보였다. 해당 모형의 성능지표는 MAPE 9.31%, RMSE 3,302, R-squared 0.927로 나타났으며, 위도․경도 정보만을 포함한 모형은 MAPE 10.63%, RMSE 4,081, R-squared 0.8969로 가장 낮은 성능을 기록하였다. 또한 경도․위도와 함께 단지 ID를 포함한 경우가 기초구역 ID를 포함한 경우보다 성능이 소폭 개선되어 MAPE 기준으로 10.21%를 기록하였다. 이러한 결과는 단지 정보와 기초구역 정보가 위도․경도와 같은 지리적 좌표만으로는 포착할 수 없는 다세대주택 가격 형성의 개별적 특성을 설명하는 데 기여함을 시사한다.
| 포함 입지 변수 | R-Squared | RMSE | MAPE (%) |
|---|---|---|---|
| [경도, 위도] 정보만 포함 | 0.8969 | 4,081 | 10.63 |
| [경도, 위도] + [단지 ID] | 0.9035 | 3,947 | 10.21 |
| [경도, 위도] + [기초구역 ID] | 0.9010 | 3,999 | 10.22 |
| [경도 위도] + [단지 ID] + [기초구역 ID] | 0.9270 | 3,302 | 9.31 |
주: MAPE값의 단위는 %이며 손실함수는 Tweedie 손실함수로 설정하여 비교함.
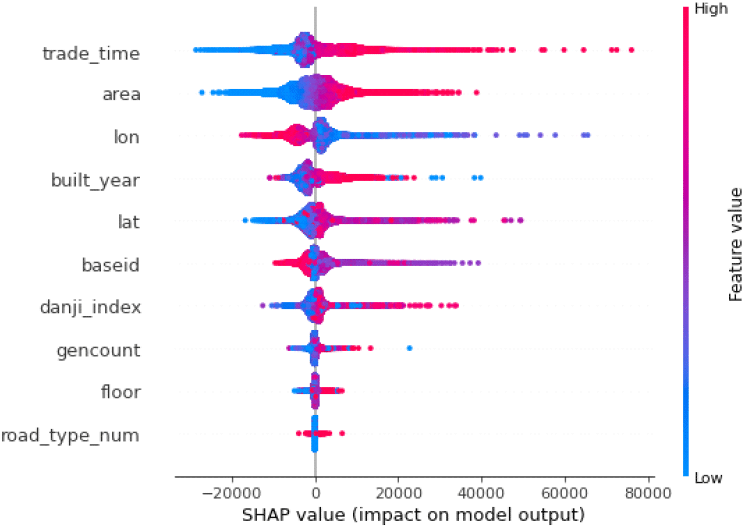
다세대주택 가격 추정 모형에서 개별 변수의 영향력을 파악하기 위하여 SHAP(shapley additive explanations) 값을 기반으로 한 요약도(summary plot)를 활용하였다(<그림 5> 참조). 해당 분석 방법은 머신러닝 예측 모델 내에서 각 설명변수가 결과 값에 미치는 영향을 시각적으로 표현하는 도구로서 특성 중요도 순으로 위에서 아래로 나열된다. 요약도의 y축은 분석에 사용된 각 설명변수의 이름을 나타내며, x축은 해당 변수의 SHAP 값으로, 0보다 크면 해당 변수가 예측값을 증가시키는 방향으로 작용한 것이며, 반대로 0보다 작으면 예측값을 감소시키는 방향으로 작용한 것으로 해석된다. 0으로부터 넓게 퍼진 형태일수록 타겟 변수인 가격에 영향을 미치는 정도가 높은 것으로 볼 수 있다.
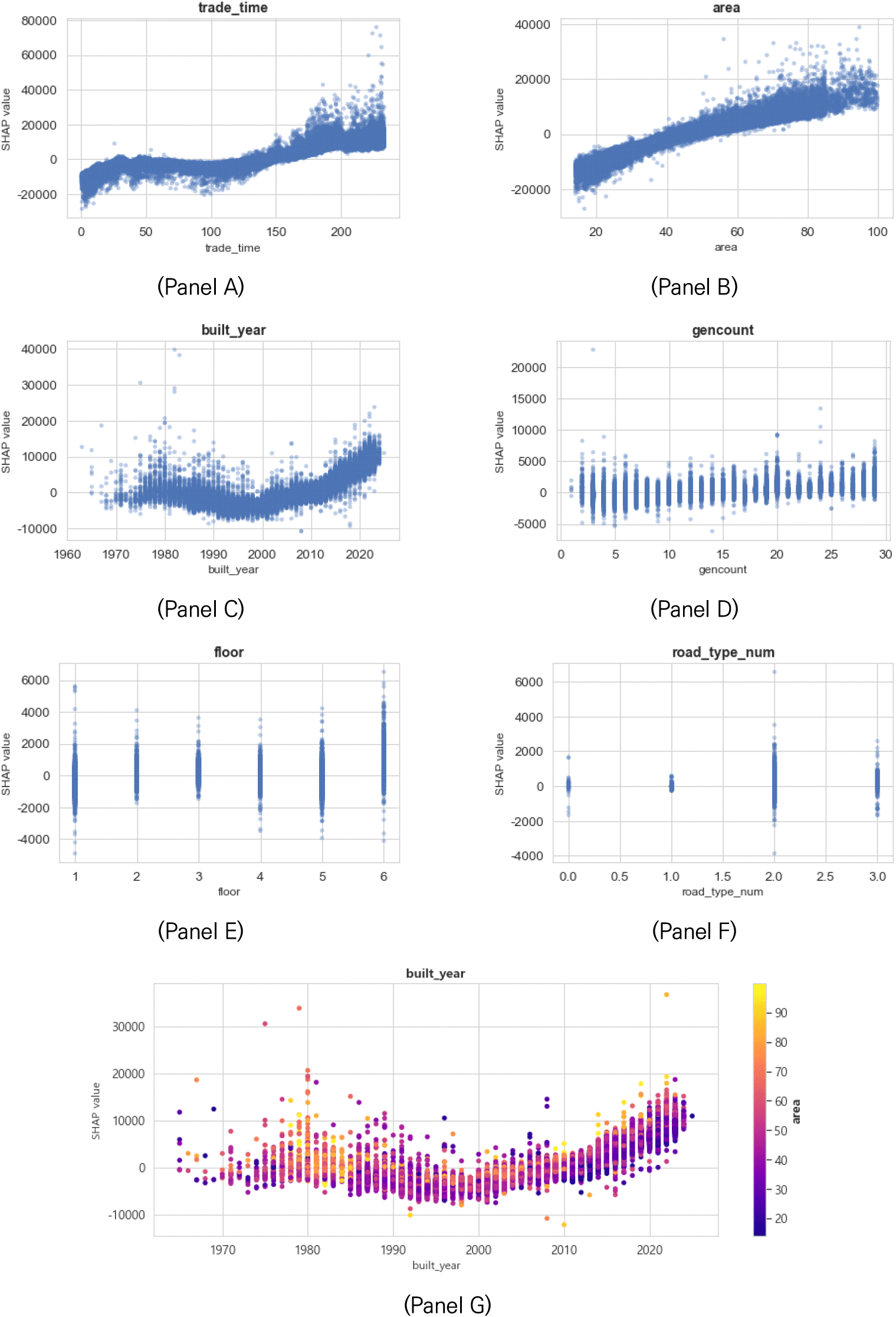
각 변수별 SHAP 값 분포는 <그림 6>과 같다. Trade_time(거래 시점) 변수는 SHAP 분석 결과에서 가장 높은 중요도를 나타내며, 이는 해당 변수가 주택 가격 추정 모형에서 가장 영향력 있는 설명 변수 중 하나임을 의미한다. SHAP 값이 전반적으로 주택 가격의 흐름과 유사한 패턴을 보이는 가운데, 특정 시점에서는 SHAP 값의 분산이 뚜렷하게 증가하는 양상이 관찰되었다. 이는 해당 시점의 시장이 상대적으로 불안정했음을 시사하며, 향후 SHAP 값의 시계열적 분산 분석을 통해 시장의 불안정성을 조기에 탐지하고, 분산이 확대되는 시점에 대해 주택 가격 대비 대출 가능 금액 조정, 거래세 완화 및 강화 등의 선제적 안정화 정책의 필요성을 제기할 수 있다.
Area(전용면적) 변수의 경우, 전용면적이 클수록 주택 가격에 정(+)의 영향을 미치는 것으로 나타났다. 이는 총 주택 가격이 면적 증가에 비례하여 상승하는 구조적 특성을 반영한다. SHAP 값 분포를 보면, 30~60m2 구간에서는 비교적 분산이 일정하게 유지되나, 면적이 60m2를 초과하는 구간에서는 SHAP 값의 분산이 크게 확대되는 양상이 나타난다. 이는 대형 주택의 경우 가격 결정에 영향을 미치는 요인이 더욱 다양하고, 이로 인해 예측값의 기여도에 대한 불확실성이 커질 수 있음을 시사한다. 이는 대형 주택에 대한 수요의 지역별 차이를 파악하는 데 중요한 설명 변수로 작용할 수 있다.
Built_year(준공연도) 변수의 경우, 가장 최근에 준공된 주택일수록 가격이 높게 나타나는 반면, 1990년대에 준공된 주택은 상대적으로 낮은 가격대를 보였다. 그러나 1970~1980년대에 준공된 주택의 경우 다시 가격이 상승하는 양상이 관찰되었으며, 전형적인 U자 형태의 분포가 나타났다. 이러한 경향은 해당 시기에 준공된 다세대주택이 재개발 요건을 충족하는 연한을 초과함에 따라 향후 재건축을 통한 가치 상승에 대한 기대감이 거래 가격에 반영된 결과로 해석될 수 있다. 이는 향후 노후율을 충족하게 될 지역들을 선제적으로 탐색하고 재개발 후보지의 과열 정도를 식별하는데에 적용될 수 있다. 아울러 인근 지역과의 상대적 비교를 통해 적정 주택 가치를 산정하고, 향후 보상 기준 자료로도 활용될 수 있을 것이다.
한편, SHAP 값의 분석을 통해 변수간의 관계를 추가적으로 파악할 수 있다. <그림 6>의 Panel G의 경우 주택 연식별 선호되는 전용면적의 차이를 보여준다. 1970~1980년대 준공된 주택의 경우 주택 면적이 높을수록 가격 상승에 기여하나, 2010년대 이후 준공된 주택의 경우 60m2 이하의 소형 주택이 거래의 대다수를 차지한다.
Gencount(단지 내 세대수) 변수의 경우, 세대수가 많을수록 주택 가격이 상승하는 방향으로 작용함을 보여준다. 이는 대규모 단지일수록 관리 효율성, 커뮤니티 형성, 다양한 부대시설 확보 등의 가능성이 높아 주거 선호도가 상승한다는 기존 연구의 결과와 일치한다. 대규모 단지 선호 경향은 도시계획 및 공동주택 개발 정책의 방향 설정에 있어 집약도와 단지 규모가 주거 선호도에 미치는 영향력을 뒷받침하는 근거가 될 수 있다.
Floor(주택 층수) 변수의 SHAP 분석 결과, 3층은 가격 기여도의 분산이 가장 낮았으며, 6층은 가장 높은 가격 상승 기여도를 보였지만 동시에 분산도 가장 크게 나타났다. 이는 1층부터 5층까지는 가격 기여도가 비교적 일정하게 유지되는 반면, 6층 이상에서는 경관, 조망권 등 추가적인 입지 요인이 작용하여 가격이 상승하는 구조를 반영한 것으로 해석된다.
Baseid(기초구역 고유번호)와 danji_index(단지 고유번호)의 경우 SHAP 값이 대체로 0에 수렴하나, 특정 변수의 경우 상승하는 추세 및 분산이 매우 높게 나타났다. 특정 기초구역 혹은 단지에 대한 SHAP 값이 예외적으로 높게 나타나는 현상은 해당 지역의 개발 기대감, 접근성 개선 등을 반영할 가능성이 있다. 이를 기반으로 소지역 단위의 정밀한 주택시장 모니터링 체계 구축를 구축하고 지역 부동산 정책의 정량적 기준으로 활용할 수 있을 것이다.
Road_type_num(주택 인접도로 분류)의 경우, “로”(‘2’, 접면도로가 12m 이상 40m 미만)와 “길(‘3’, 12m 이하)”의 경우 모두 대체로 가격추정에 기여하였고, “대로”(‘1’, 접면 도로가 40m 이상)와 그 외 도로명주소가 없어 분류 불가능하여 0으로 코딩된 경우, 가격추정에 소폭 기여하는 것으로 나타났다. 도로 접근성과 가격 기여도 간의 관계는 기반시설 개선 사업의 타당성을 평가하거나, 소규모 노후주택지 정비계획 수립 시 정책 우선순위를 설정하는 데 활용될 수 있다.
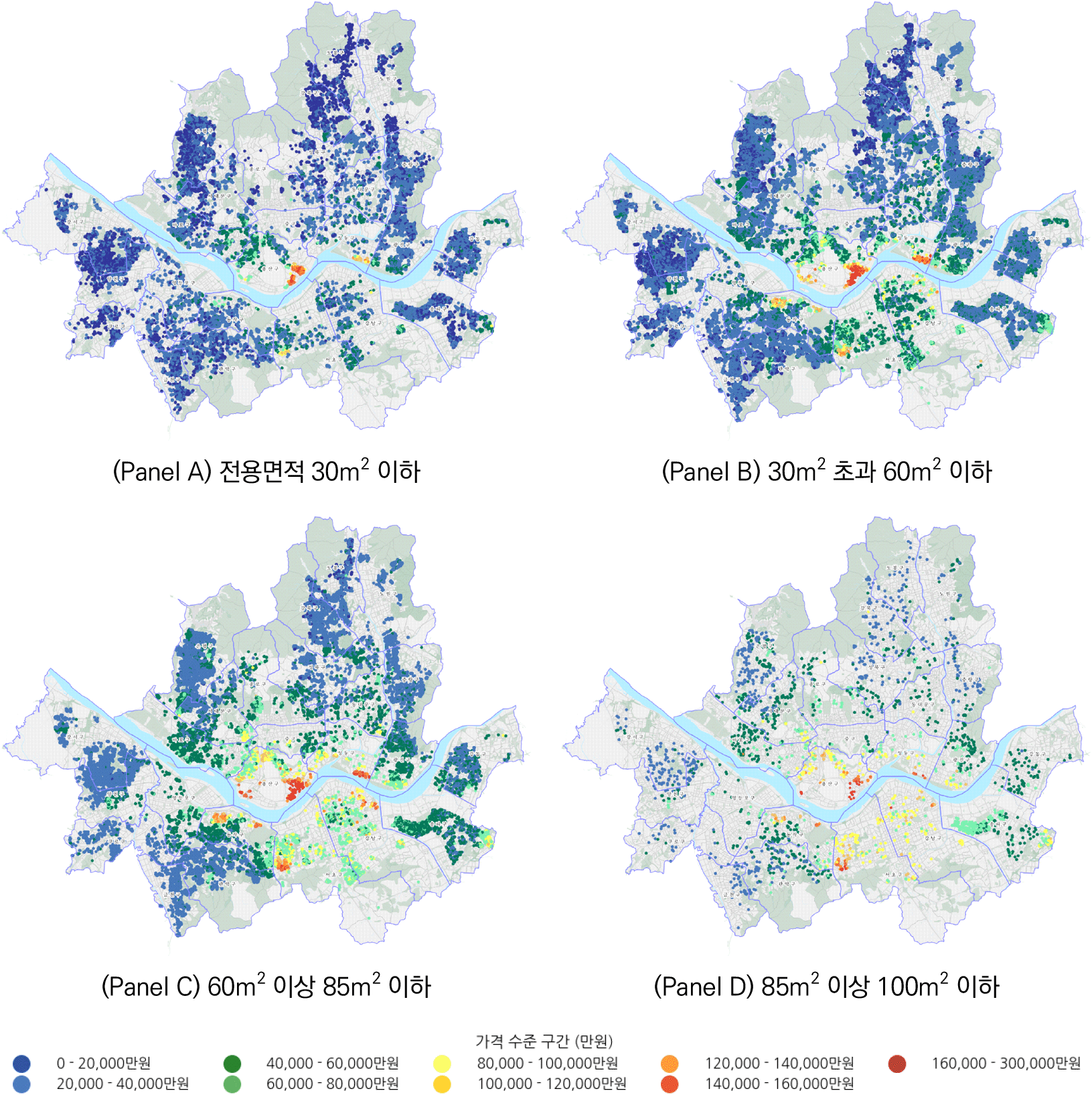
다세대주택의 시장 세분화를 구체적으로 살펴보기 위하여 전용면적 구간별로 30m2 이하(초소형주택), 30초과 60m2 이하(소형주택), 60 초과 85m2 이하(중소형 주택), 85 초과 100m2 이하(중형주택)으로 구분하여 개별 다세대주택의 가격 수준(단위: 억 원) 검토하였다(<그림 7> 참조). 전반적으로 모든 면적대에 있어 높은 가격대에 해당하는 주택은 강남구와 서초구에 집중되어 있는 것으로 나타났다. 이들 지역은 고급주거단지와 주거 인프라가 갖추어져 있으면서 주요 업무지구와의 접근성에 대한 효용을 제공하는 지역으로 설명될 수 있다.
한편, 유독 높은 가격대를 형성하고 있는 구역이 나타나는데 이는 재개발 논의가 활발하게 이루어지고 있는 한남동 일대의 재개발구역과 성수전략정비구역 등 한강변 고급 주거지역으로, 아직 정비가 본격화되지 않았음에도 미래 가치가 선반영되며, 투기적 수요 및 고소득층 선호가 복합적으로 반영된 것으로 파악된다.
한편 서울 외곽에 위치할수록 전반적으로 저가 주택이 집중되는 것으로 나타났다. 서울 내 다세대주택 시장에서 고가와 저가주택의 분포가 명확하게 나뉘어 자산 가격이 양극화하고 있음을 보여준다.
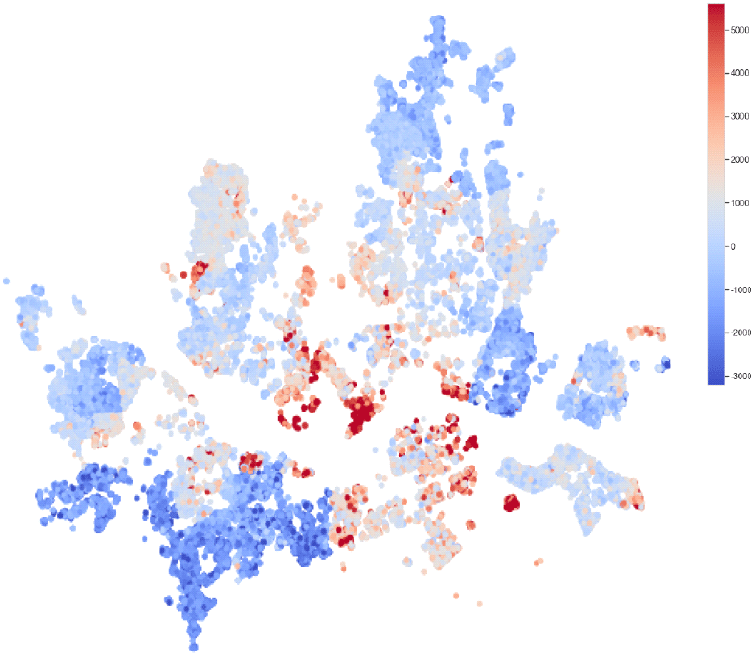
이러한 지역별 자산 가격 격차는 단지 고유번호 변수의 투입을 통해 각 고유번호가 주택가격 모델링에 기여한 정도를 파악한 SHAP 값의 지리적 분포를 통해서도 드러난다(<그림 8> 참조). 관악구, 동작구, 광진구, 노원구 및 도봉구, 양천구 등 서울 외곽에 소재한 단지들은 재건축․재개발 기대가 낮거나, 교육․교통․생활 인프라 부재 등으로 인한 매매 수요 위축, 거래량 감소로 인해 가격이 하락하는 방향으로 모형에 기여하였음을 나타낸다. 이들 지역의 가격 상승은 상업시설, 교통 인프라, 학군, 인접 아파트 등 주변 환경과의 연계성에 기인한 것으로 추정되며, 향후 이들 요인과의 정량적 연관성을 지역별로 분석함으로써 보다 실증적인 지역 가격 동학 해석이 가능할 것이다.
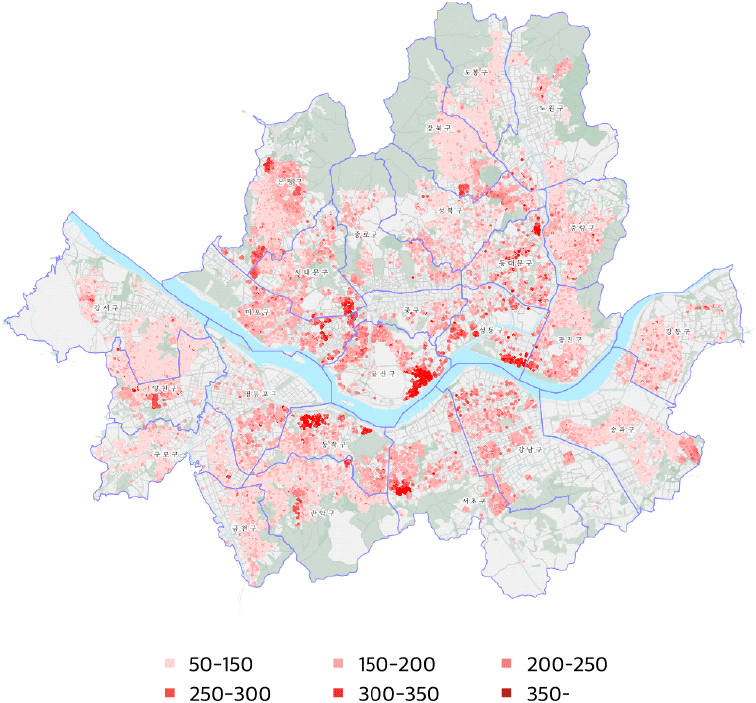
<그림 9>는 다세대주택 단지별로 가격변화를 지수화하여 공간적 분포로 나타낸 것이다. 머신러닝 추정모형을 활용하여 개별 주택별로 가격 변화율을 산정하였을 때 공간적 패턴이 뚜렷하고 해상도가 높은 주택 변화 양상이 도출되고 있음을 확인하였다. 특히 높은 상승률을 보이는 주택들이 특정 지역을 중심으로 밀집하고 있음을 확인하였다.
가장 높은 가격상승률을 보인 지역은 용산구의 한남재개발구역, 성동구의 성수전략정비구역, 서초구의 방배주택 재개발 정비사업, 동작구의 흑석정비촉진구역과 노량진 재정비촉진지구, 관악구의 신림재정비지구 등으로 파악되었다.
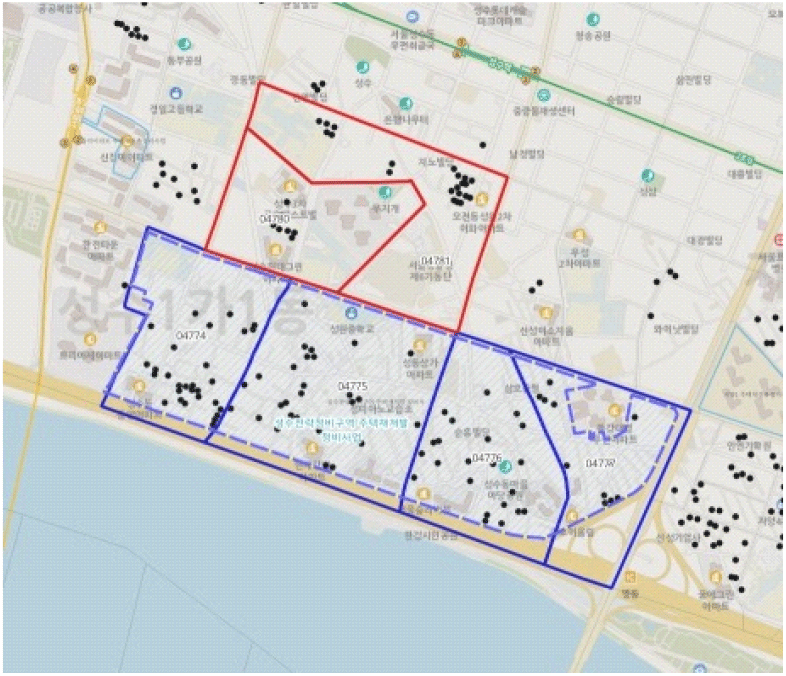
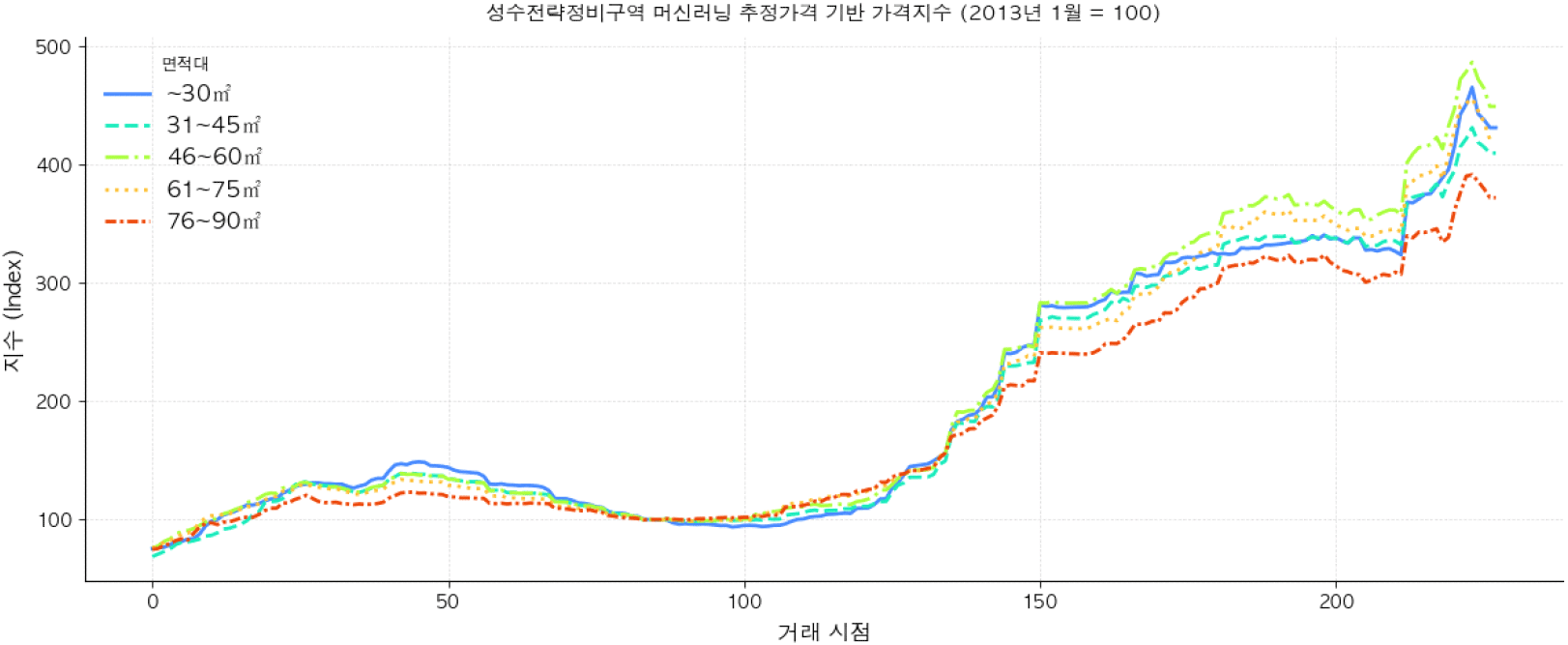
소지역 단위 지수의 산정단위가 되는 개별주택의 추정가격이 실제의 가격흐름을 잘 반영하는지 여부를 구체적으로 살펴보기 위하여 현재 재정비 논의가 활발하게 이루어지고 있는 한강변 구역 내 주택과 구역에 포함되지 않은 인접 지역의 주택의 가격흐름을 비교하였다. 사례지역으로, 한강변에 위치하여 개발 압력이 심한 공간으로서 다양한 유형의 주거유형이 혼재되어 있는 서울시 성동구 성수전략정비구역 내 구역과 밖에 소재하는 주택을 비교하였다. 성수전략정비구역7) 에 위치한 기초구역(04774~04777)과 구역 밖에 위치한 기초구역(04780~04781)에 대하여 각 구역에 소재한 다세대주택의 가격변화양상을 구체적으로 비교하였다. 각 구역도는 <그림 10>에 나타난다.
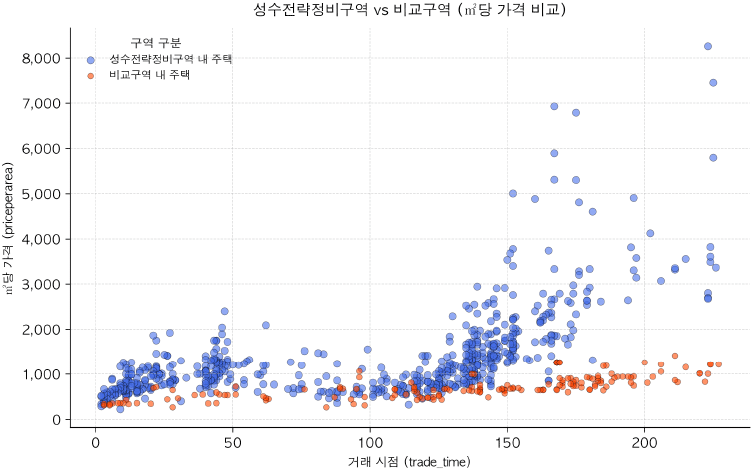
구역 내 위치한 주택들의 실제 가격추이(를 살펴보면 정비구역 내 소재한 주택의 총 거래건수는 157건으로, 면적당 가격이 2006년 1월을 기준으로 약 400만 원/m2에 거래되다가 2009년에 1,500만 원/m2대까지 상승 후 2012년에 다시 400만 원/m2대로 복귀하였다. 이후 2014년부터는 2021년까지의 기간 동안에는 최고가를 기준으로 2006년의 5~6배 가격까지 상승하였는데 해당 기간은 저금리 기간으로 부동산 상승 시장의 흐름과 본격적인 투자 압력이 반영된 것으로 보인다. 2021년 4월 토지거래허가구역8) 으로 지정된 이후에는 거래가 활발하게 이루어지지 않고 있다.
이에 반해 인접 비교구역(거래건수 총 107건)에서는 정비지구에 비하여 다소 안정적인 상승흐름을 보이고 있으며, 시장이 안정되기 시작한 2013년 1월을 기준으로 마지막 거래가 된 2021년 상반기까지 약 2~2.5배 상승한 것으로 파악된다(<그림 11> 참조).
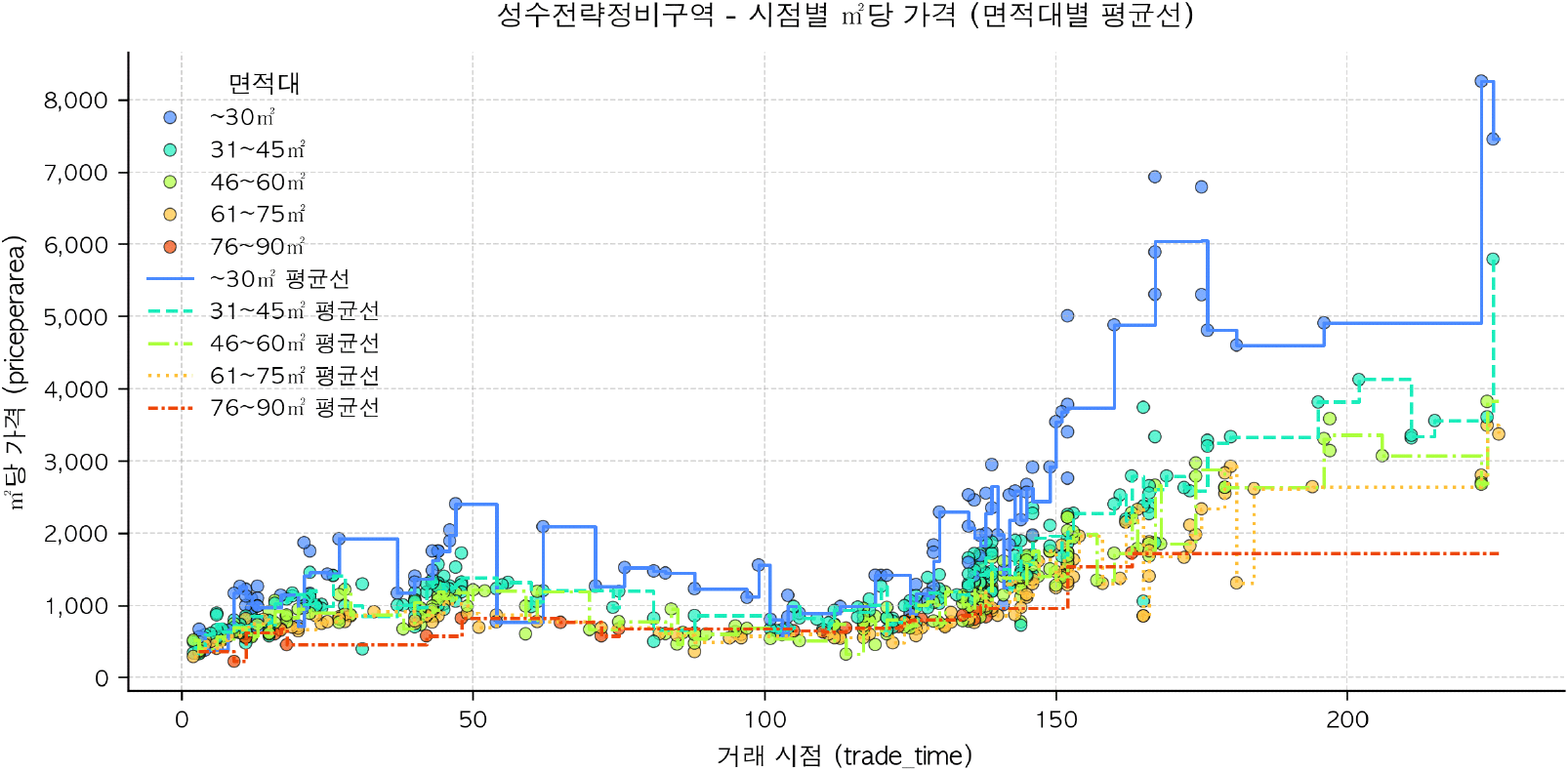
성수전략정비구역 내에는 87개 다세대주택 단지가 소재하고 있으며 총 624세대로 이루어져 있다. 해당 주택의 면적 구분별로 평균선의 흐름을 산출하였으며 해당 거래가 없는 기간에는 직전 가격을 연장하여 도식화하였다(<그림 12> 참조). 가격 산점도만 고려할 경우 해당 면적대의 가격흐름이 직전 매우 불안정한 가격흐름이 나타나는 것을 보여준다. 이는 가격산점도만을 기준으로 가격을 파악할 경우, 거래가 없는 기간의 경우 직전 가격을 기초로 삼거나 인근지역의 시세를 참고할 수 밖에 없어 결과적으로 시장 참여자 간 정보에 대한 비대칭성이 발생할 수 있는 상황을 보여준다.
머신러닝으로 추정한 가격의 경우 실질적으로 거래가 이루어지지 않는 토지거래허가구역 지정 기간임에도 안정적인 가격흐름을 반영하고 있는 것으로 나타난다(<그림 13> 참조). 이 기간의 가격은 2006년 시점을 기준으로 2024년 12월까지 약 4배~4.5배 상승하였으며 이는 <그림 10>에서 확인한 가격 상승 추세를 유사하게 근사하는 것으로 파악된다.
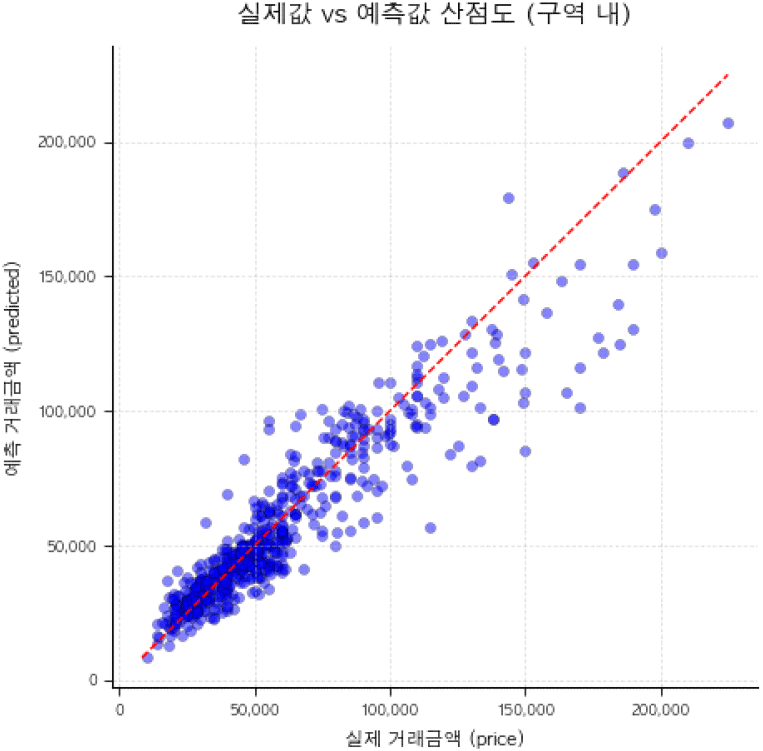
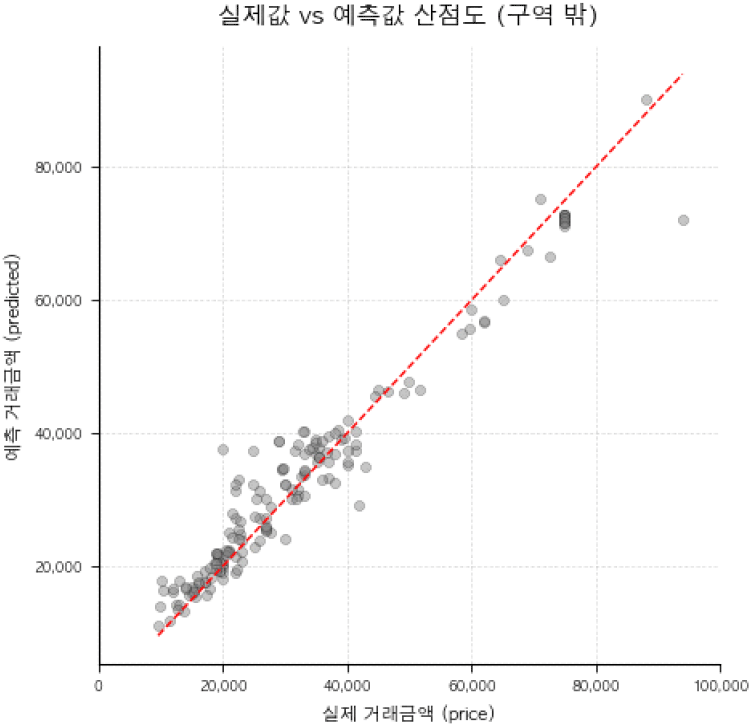
성수전략정비구역과 인접 비교구역에서 실제값과 추정값의 오차를 도식화한 산점도는 <그림 14> 및 <그림 15>와 같다. 성수전략정비구역 내의 경우 평균백분율오차(MAPE)가 10.31%, 인접 비교 구역의 경우 6.23%로 도출되어, 머신러닝으로 추정한 가격이 실제의 가격 흐름을 우수하게 반영하고 있는 것을 확인하였다. 또한, 특히 공간적 정보를 반영함에 있어 재정비촉진지구 등 정비구역의 정보를 머신러닝에 투입하지 않았음에도 기초구역이라는 공간 고유단위의 투입을 통해 인접지역과 차별화되는 외부적 요인에 따른 소지역 효과를 우수하게 반영하는 것으로 판단된다.
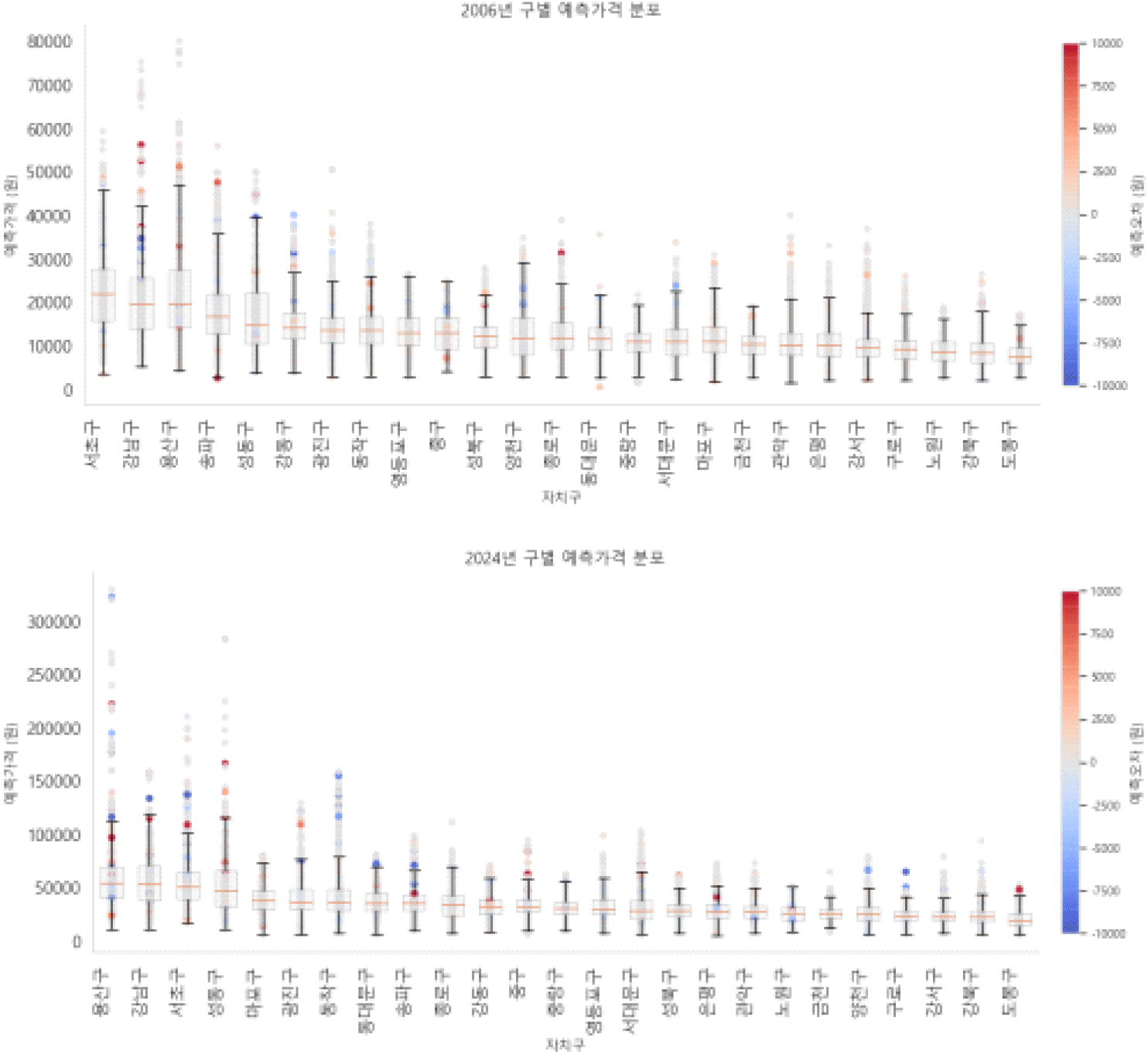
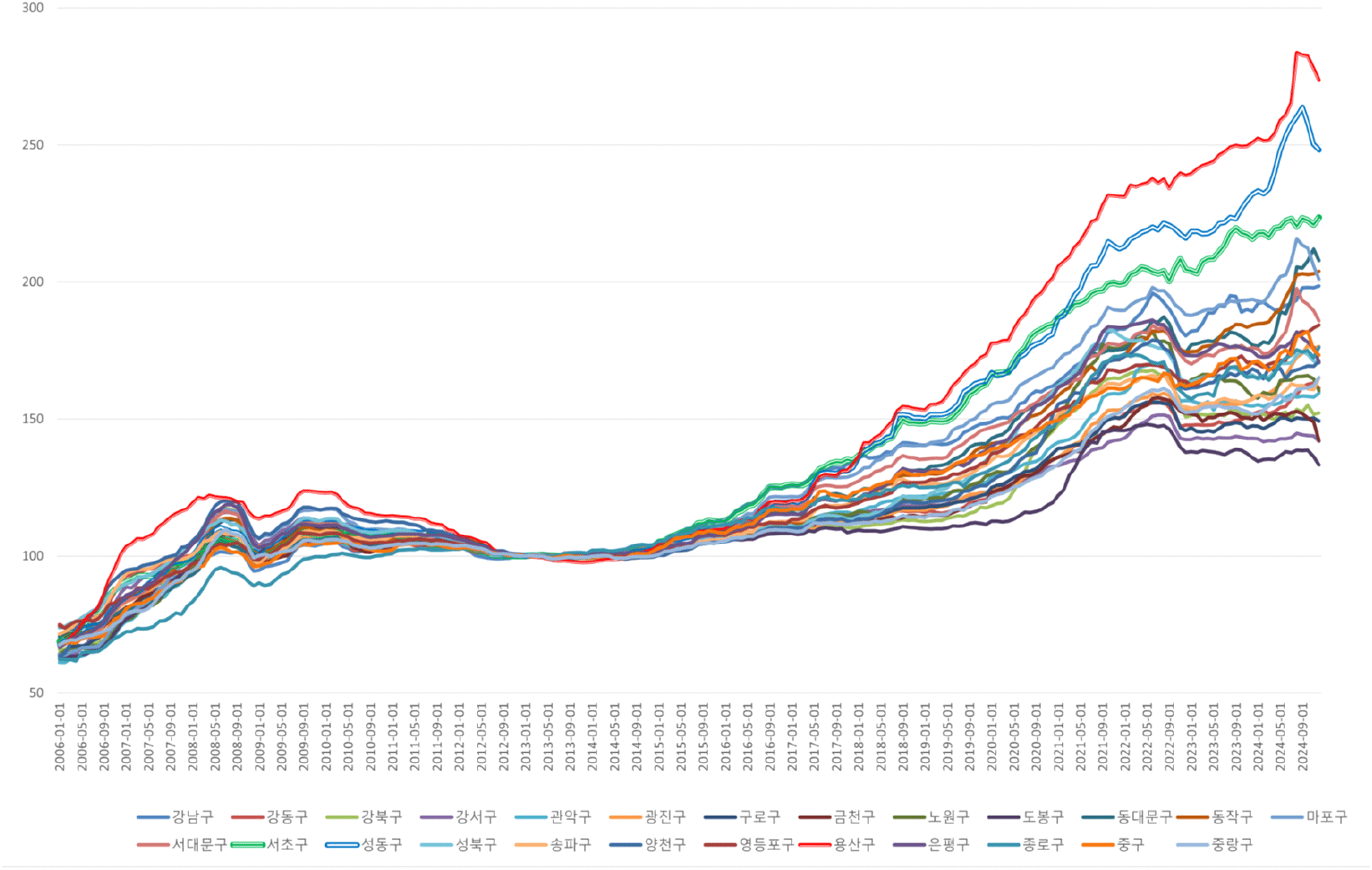
앞서 기술통계에서 확인한 것에 따르면 2006년 대비 2024년의 중위가격 상승률은 약 2배, 2013년 대비 2024년의 상승률은 1.66배로 집계된 바 있다. 본 절에서는 가격지수 산정의 최초연도인 2006년과 마지막 연도인 2024년을 기준으로 자치구별 중위 가격과 순위의 변화를 살펴보았다(<그림 16> 참조).
2006년 자치구별 중위가격은 서초구, 강남구, 용산구 순이었으나, 2024년 자치구 순위는 용산구, 강남구, 서초구, 성동구 순으로, 용산구가 가장 높은 것으로 나타났다. 전반적으로 상위 4개 구의 분산이 매우 높게 형성되며, 해당 구 외의 구는 대체적으로 유사한 양상을 보인다. 다른 서울에 소재한 자치구별로 2013년 1월을 기준으로 2024년 12월의 가격지수를 산정 후 비교 검토한 결과, 용산구(273.64), 성동구(248.25), 서초구(223.51) 순으로 높은 것으로 산정되었다. 이는 해당 구에 앞에서 다룬 것처럼 재개발논의가 활발한 지역의 다세대 가격 상승률이 반영된 것으로 파악된다(<부록 표 1> 및 <부록 그림 1> 참조).
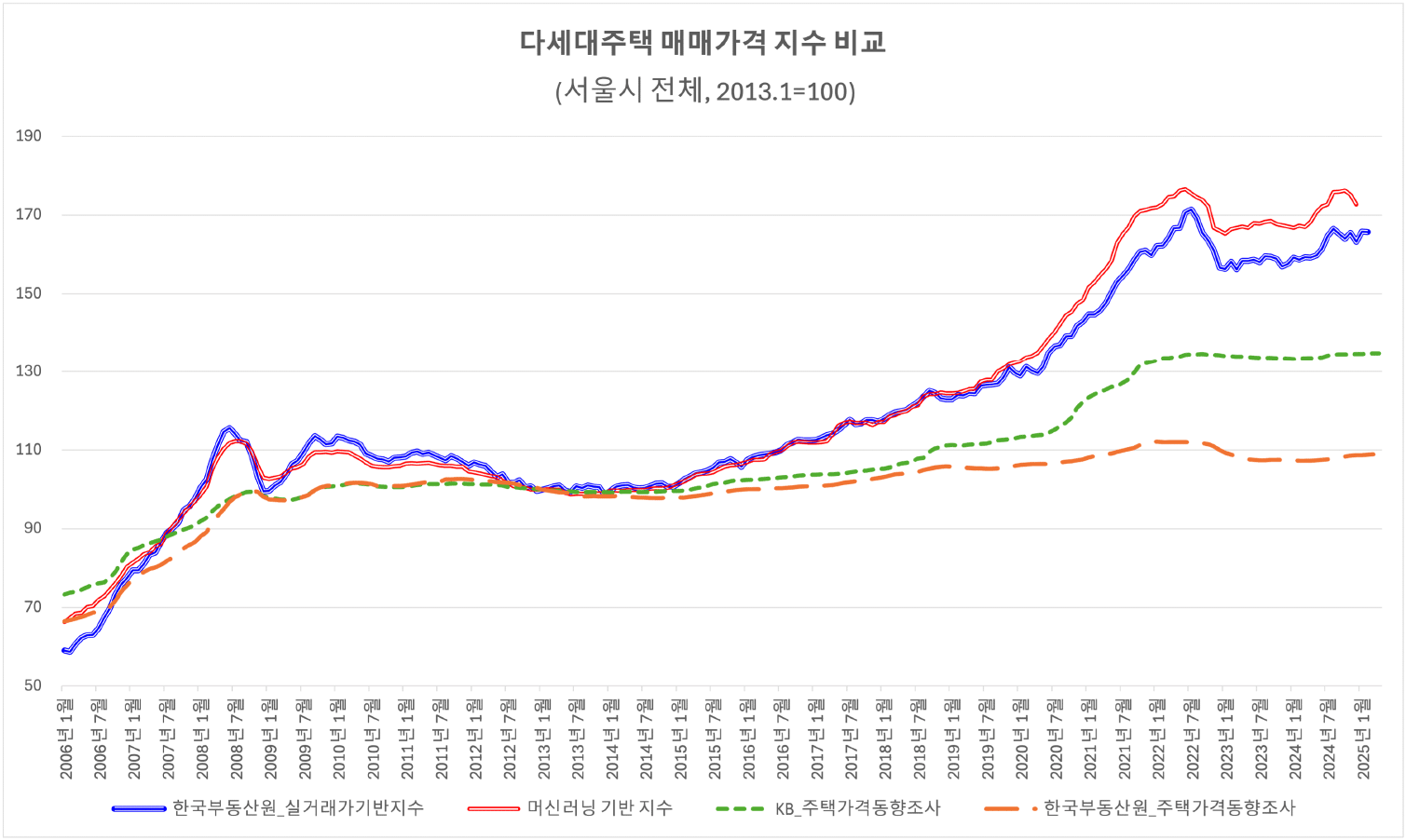
본 절에서는 다세대주택에 대하여 산정한 머신러닝 기반 지수를 누적 가격 상승률 측면에서 한국부동산원의 공동주택 실거래가격지수와 주택동향지수, KB 주택가격동향조사에서 산정된 연립다세대 가격지수와 비교하고, 차이의 발생 원인을 고찰하였다. 한국부동산원 주택가격동향조사의 연립다세대의 지수의 경우 해당 기간 누적상승률은 108.65로 거의 상승하지 않은 반면, 같은 작성기관의 공동주택 실거래가격지수의 경우 163.17로 나타나 기반하고 있는 가격의 성격에 따라 누적 상승률이 매우 다르게 나타나고 있음을 알 수 있다(<표 8> 참조).
주: KB 지수는 강북 14개구와 강남 11개구에 대하여 연립 매매가격지수를 제공하여 강북권에 해당하는 도심부, 서북권, 동북권에 해당하는 지수와 비교할 수 있다.
본 연구에서 산정된 머신러닝 기반 지수는 실거래가격지수와 유사한 정도의 누적 상승률(172.71)을 보인다. 특히 2020년 이전까지는 유사한 가격 상승률을 보이다가 부동산 시장 상승기인 2020년 이후부터는 상승폭이 더 크게 나타나게 된다(<그림 17> 참조). 이는 실거래가격지수가 각 주택 상승률을 기하 평균하여 산출하는 제본스 방식을 사용하는 반면, 본 연구에서 작성된 머신러닝 기반지수는 라스파이레스 지수로 산정하여 고가 주택의 상승률이 더 크게 반영된 결과로 볼 수 있다.
생활권별로 비교할 경우, 머신러닝 가격이 도심부의 경우 가장 높게 나타났으나(240.22) 한국부동산원의 주택가격동향조사에서는 서북권의 가격지수가 가장 높게 나타났다(114.78). 또한 KB 주택가격동향조사에서는 강북14개구(135.64)의 누적상승률이 강남11개구(133.71)에 비하여 미세하게 높게 나타났다.
타 기관 작성 지수와 본 연구의 머신러닝 기반지수의 차이가 발생하는 이유로는 첫째, 통계 표본의 차이로 볼 수 있다. 구체적으로, 한국부동산원의 주택가격동향조사의 경우 연립다세대주택의 표본이 전국단위로 약 6,626호가 포함되며 KB지수의 경우 연립다세대주택의 표본이 전국 2,500호(서울 840호)가 포함되나, 본 연구에서는 총 71,970개 단지(약 65만 호)에 대한 다세대주택을 포함하고 있다는 점에서 지수의 차이가 발생할 수 있다. 또한, 타 기관 작성 가격지수에는 연립주택에 대한 지수가 포함된다는 점에서 차이가 발생할 수 있을 것이다.
둘째, 가격 조사 기간의 차이가 발생한다. 한국부동산원 가격동향조사와 KB주택가격동향조사 지수는 조사평가기반 지수로서, 한국부동산원 가격동향 조사의 경우 조사 기준시점이 익월 1일, KB지수의 경우 매월 15일이나, 본 연구에서는 기준시점이 해당 월의 모든 거래건수를 모형에 투입시켜 해당 월의 지수로 산정하기 때문에 조사 시점에 따라 지수의 차이가 발생할 수 있다.
셋째, 매물 가격 반영여부에 따른 차이가 발생한다. 특히, 한국부동산원은 주택가격동향을 산정함에 있어, 당해 월 조사 대상의 실거례 사례가 없는 경우, 동일 단지의 유사 거래 사례와 매물 가격, 부동산 중개 업소의 의견을 종합적으로 참고하여 표본의 가격을 산정하게 된다. 이때 조사자․평가사의 주관이 개입되어 시장 침체기에는 보수적으로 평가하거나, 일정 시차가 발생하게 되는 경우가 평활화 현상으로 나타난다는 점이 다수의 선행연구에서 제시된 바가 있다(김현영 외, 2018; 박연우․방두완, 2011).
본 연구에서 산정한 다세대주택 가격지수는 표본 수 측면과 조사 시점 측면에서 더 많은 표본을 포함하며, 이는 앞 절에서 검토한 중위값의 가격 추이를 통해 파악한 것과 같이 현실의 누적 상승추세를 반영하는 것으로 결론내릴 수 있다. 또한, 생활권별, 구별, 기초구역 단위별 가격지수 등 다양한 공간권역별 지수를 산정할 수 있다는 점에서 유용하다.
V. 결론
본 연구는 비아파트 유형으로서 연구가 미진했던 다세대주택 매매시장에 대하여 정확한 주택가격 지수 산정의 필요성을 인식하고, 머신러닝방법을 활용하여 서울시와 세부 지역별로 가격지수를 산정할 수 있는 가능성과 유용성을 검토하였다. 기존 가격지수가 거래가 없는 기간과 소지역 효과를 포착하지 못하는 한계를 극복하기 위하여 본 연구는 머신러닝 모형을 통해 개별 주택 단위에서의 가격을 추정하고 이를 기반으로 다양한 소지역 단위의 가격지수를 산정하였다.
본 연구의 실증 결과, 머신러닝 기반 가격 추정가격을 활용한 지수 산정은 고해상도의 가격 수준과 변화 양상을 파악하는 데 효과적임을 확인하였다. 하위시장 식별에 장점이 있는 트리 기반의 LightGBM 모형을 구축함에 있어 공공데이터로 공시가격 단지정보와 공시가격 공간정보, 실거래가격을 활용하였으며 손실함수 및 최적 패러미터 설정을 통하여 모형의 성능은 평균절대오차(MAPE) 값 기준 9.31% 수준으로 파악되었다. 또한 머신러닝 모형의 산정에 있어 위도․경도 외에도 단지 고유번호와 기초구역 고유번호를 투입하여 입지 정보를 효율적으로 포착할 수 있음을 확인하였다.
이후 머신러닝 모형으로 추정한 다세대 주택 가격의 공간적 분포를 통해 다세대 주택의 가격의 수준과 상승률 측면에서 모형의 유용성을 검증하였다. 가격 수준 측면에서 고급주거지와 도심접근성, 양호한 주거 및 교육 인프라를 지닌 강남구와 서초구에 높은 가격대가 집중되어 있으며, 가격 변화 측면에서는 재개발 논의가 활발한 재정비촉진지구 등에서 인접지역과 차별화된 가격 변화를 포착할 수 있었다. 특히 성수전략정비구역 사례 분석을 통해 소지역 단위 지수의 유용성을 검증하였다.
자치구별로 산정한 가격지수를 분석한 결과, 재정비촉진지구 등이 포함된 일부 자치구에서 상대적으로 높은 누적 상승률이 나타났다. 또한 본 연구의 머신러닝 기반 지수를 타 기관의 매매가격지수와 비교한 결과, 한국부동산원의 ‘전국주택가격동향조사’ 및 KB국민은행의 ‘주택가격동향조사’와 같은 조사․평가가격 기반 지수는 동일 기간 동안 상대적으로 현저히 낮은 상승률을 보인 반면, 실거래가격 기반 지수는 본 연구의 지수와 유사한 수준의 높은 누적 상승률을 기록하였다. 이는 머신러닝 기반 지수가 실거래 가격의 변동을 효과적으로 포착하여, 실제 시장 가격 변화를 보다 정확하게 반영하고 있음을 보여준다.
본 연구에서 산정된 생활권별, 구별, 기초구역 단위별 가격 지수는 임대차 보호, 공급 정책, 시장 안정화 등의 정책 설계 측면에서 다음과 같이 향후 다양한 연구에 활용될 수 있다. 먼저 공공이 다세대주택을 매입할 경우 적정가격 산정에 참고 할 수 있다. 또한, 노후 저층 주거지에서 투기적 시장을 선제적으로 탐지하고, 더 나아가, 머신러닝 추정 주택 가격과 전세가격과의 비교를 통한 깡통전세 탐지(김기중 외, 2023) 등 부동산 사기 방지와 임대차 보호 정책 수립 등에 활용할 수 있을 것이다.
다만 본 연구에는 몇 가지 한계도 존재한다. 첫째, 멸실 추정, 주소지 누락 등으로 지수 산정 대상에서 제외된 다세대주택은 포괄하지 못하였다. 이로 인해 특히 재개발사업으로 다른 건축 유형으로 된 구역 또는 주택이 있을 경우 표본 누락이 발생하며, 이는 지수의 시장가치 반영 측면에서 제약 요인으로 작용한다. 또한 가격 공시정보가 다세대주택에 대한 정보만 제공함에 따라 연립주택을 가격지수에 포함하지 못하여 타기관 지수와의 비교 시 제약사항으로 작용하였다. 이러한 데이터의 누락은 향후 다년간의 다세대주택 공시가격 정보의 확보, 누적 및 병합으로 지수의 안정성과 신뢰성이 보완될 수 있을 것이다.
둘째, 인접 지역간의 가격 흐름의 차이를 실증적으로 보여주기 위하여 성수전략정비구역과 인접 지역의 가격 상승 추이를 검토하였으나, 이는 사례로서, 주택정비사업의 유형, 구역의 규모, 대상 주택의 규모, 용도지역, 용적률 인세티브 여부에 따른 효과를 종합적으로 검토하지 못하였다. 다세대주택 밀집지역의 물리적 노후화가 임계점에 도달하면서 가격 변화 동학을 구체적으로 파악하기 위하여 명시적으로 재개발이 확정된 지역 외에도 소규모 재개발, 신속 통합기획, 모아타운, 소규모 재개발, 빈집 개선 사업 등 현재 시행되고 있는 다양한 도시정비 사업 체계와 과거 시행 이력이 해당 지역에 어떠한 영향을 미치는지 입체적으로, 또 미시적 단위에서 해석할 필요가 있다.
셋째, 가격추정모형 내 실거래가에 대지권 정보를 정교하게 반영하지 못한 점 역시 한계로 지적된다. 동일 단지 내에서도 대지권 비율, 향, 층고, 조망권 등 차이에 따른 가격 격차가 존재함에도 불구하고, 이를 충분히 설명하지 못하여 주택 간 가격 차이가 과소 또는 과대 평가될 위험이 있다. 이는 현재 구득 가능한 공공데이터의 한계로 인하여 직접적으로 반영되지 못한 것으로, 이는 향후 집합 건물 대장, 등기부등본 정보 등과 병합 후 각 주택별로 할당된 대지권 정보를 연계하여 활용할 수 있을 것이다.
마지막으로, 다세대주택 중 2010년 이후 공급된 도시형생활주택과의 혼재 문제 역시 향후 보완이 필요한 과제로 남아 있다. 도시형 생활주택의 경우 고층 오피스텔의 형태로서 일반적인 저층 주거지 내 다세대주택과 차별화된 수요를 가질 수 있기 때문에, 이를 식별할 수 있는 명확한 알고리즘이 요구된다.
향후 연구에서는 단독․다가구주택까지 분석 대상을 확장하여, 도시 저층주거지 전반에 대한 시계열의 안정성을 검증하고 다양한 정책 시뮬레이션에 활용될 수 있도록 정밀한 시장 분석을 수행할 필요가 있다. 구체적으로는 인접 아파트 가격, 주요시설 및 교통 접근성 변화, 인구변화 등이 다세대주택에 미치는 영향을 개별 분석(case-study)등 실증적으로 규명함으로써 시장 구조에 대한 이해를 심화시키는 것이 중요한 과제가 될 것이다. 본 연구의 고해상도 가격지수는 단순한 시장 정보 제공을 넘어서 다양한 정책적 개입의 기초자료로서 활용될 수 있을 것으로 기대된다.