Ⅰ. 서론
이자율은 주택시장에 영향을 미치는 가장 중요한 거시 경제변수 중의 하나이다. 1980년대 중반의 미국의 저축대부조합 사태, 2000년대 초반의 범세계적 주택가격 급등, 금융위기의 발단이 된 2007년의 서브프라임 모기지 사태 등은 모두 이자율과 주택가격의 밀접한 관련성을 보여준다. 이자율과 주택가격의 관계에 관한 이론적 논의는 비교적 간단하다. 현재가치 이론에 의하면, 모든 자산가격은 이자율의 움직임과 반대 방향으로 움직인다. 주택도 하나의 자산이며, 따라서 이자율이 상승하면 주택가격은 하락하고, 반대로 이자율이 하락하면 주택가격은 상승하게 될 것이다. 문제는 이자율변동이 주택가격에 미치는 영향이 시간을 두고 어떻게 나타나는가를 동태적(dynamic)으로 파악하는 일이다.
이자율과 주택가격의 동태적인 상호 관련성에 대한 실증적 분석은 주로 벡터자기회귀(VAR) 모형을 통해 이루어져 왔다. Sims(1980) 이후 경제분석 모형의 근간으로 자리 잡은 VAR 모형은 충격 반응함수 분석과 분산분해 분석을 통해 변수 간의 동태적 관련성을 수치로 표현할 수 있는 장점이 있으며, 이에 따라 Iacoviello(2000)를 위시한 많은 국내외 논문들이 이자율과 주택가격의 관련성을 분석하는데 VAR 모형을 원용하였다.1)
VAR 분석에서 통상적으로 사용되어 온 모형은 단일국면(one regime) 모형이다. 국면변화가 허용되지 않는 단일국면 모형은 선형(linear) 모형으로서, 변수 간의 동적 관련성이 시점이나 국면에 상관없이 일정하다. 그러나 주택시장 참여자들의 행동이 시장 국면에 따라 달라지고, 이에 따라 변수 간의 동태적 관계도 국면에 따라 달라질 수 있음을 고려한다면, 단일국면 모형에 의한 분석결과는 현실과 괴리된 결과일 수 있다.2)
본 연구에서는 VAR 모형에 마르코프 국면전환(Markov regime switching) 모형을 연계시킨 MS-VAR(Markov-switching vector autoregressive) 모형을 통해,3) 이자율변동이 주택시장에 미친 동태적 효과가 국면별로 어떠한 차이를 보이는가를 실증적으로 검토하고자 한다. 외국의 경우, 이자율과 주택가격의 동태적 관계를 MS-VAR 모형을 이용하여 분석한 논문들이 여러 편이 있으나, 우리나라에서는 아직 발표된 논문이 없다는 점에서 본 연구의 의의를 찾을 수 있을 것이다.4)
본 연구에서 분석의 초점은 두 가지이다. 첫째는, 주택시장에 미치는 이자율변동의 영향이 국면별로 차이가 있는가를 검정하는 것이며, 둘째는, 주택시장에 미치는 이자율변동 효과가 국면에 따라 얼마나 달라지는가를 구체적인 수치를 통해 살펴보고, 그 결과를 기존 연구와 비교하는 것이다. 국면별 차이 여부에 대한 검정은 모형 간의 우도비 검정(likelihood test)을 이용하며, 국면별 이자율변동 효과는 국면별 충격 반응함수와 분산분해를 통해 살펴보았다.
본 연구에서 국면은 통상적인 국면전환 모형 분석에서와 같이 고변동성과 저변동성의 2개 국면으로 구분하며, VAR 모형은 실질 주택가격, 주택거래량, 주택담보대출금리의 세 개 변수로 구성하였다. 주택가격과 거래량은 주택시장의 변수로 그리고 주택담보대출금리는 이자율 변수로 사용되었다. 소득이나 물가 같은 거시경제변수를 모형에 부가하여 분석결과의 정치성을 높일 수도 있겠으나, MS-VAR 분석에서는 변수가 많아지면 모형 추정(estimation)이 어려워지는 문제가 발생할 수 있으며,5) 변수 확대의 효과가 본 연구에서의 분석결과를 훼손시킬 정도는 아닐 것으로 여겨져 통제변수로서의 거시경제변수는 고려하지 않았다.6)
본 논문의 구성은 다음과 같다. Ⅰ장은 서론이다. Ⅱ장은 선행연구에 대한 개관으로 국면전환모형을 이용하여 주택가격과 이자율의 관계를 살펴본 국내외 실증 분석연구들과 분석결과를 정리한다. Ⅲ장은 연구방법에 대하여 설명한다. MS-VAR 모형 및 추정방법, MS-VAR 모형에서의 충격 반응함수에 대한 신뢰구간 계산 방법 등에 대하여 약술하였다. Ⅳ장은 실증 분석결과이다. 모형 추정결과와 국면 구분 관련 분석결과를 설명하였으며, 주택시장에 대한 이자율변동의 동적 파급효과를 충격 반응함수와 분산분해를 통해 국면별로 살펴보았다. Ⅴ장은 결론이다.
Ⅱ. 선행연구
마르코프 국면전환 모형을 이용하여7) 이자율이 주택시장에 미치는 영향을 분석한 실증연구는 두 가지 범주로 나눌 수 있다. 첫째는 주택가격 단일방정식에 국면전환을 적용한 연구이며,8) 둘째는 VAR 모형에 국면전환을 적용한 MS-VAR 연구이다.
첫째 범주에 속하는 국내 연구로는 김대원·유정석(2014), 전해정(2017) 등이 있다. 김대원·유정석(2014)은 주택가격지수 변동성9)을 종속변수로, 그리고 물가상승률, 고용률, 인구증가율, 이자율(회사채수익률)을 설명변수로 하는 회귀방정식에 국면전환모형을 적용하였다. 1987년 1월부터 2013년 11월까지의 월간 자료를 이용한 추정결과는, 변동성이 높은 국면에서는 금리 하락이 주택가격지수의 변동성을 높이지만, 변동성이 낮은 국면에서는 금리 하락이 주택가격지수의 변동성을 낮추는 것으로 분석하였다. 전해정(2017)은 종속변수로 서울시의 주택가격지수 증가율을, 그리고 설명변수로는 물가, 인구, 실업률, 금리(CD금리)를 사용하였다. 분석결과는 불황국면(저변동성 국면)에서는 금리가 주택가격에 유의적인 양(+)의 영향을 미치며, 호황국면(고변동성 국면)에서는 실업률이 유의적인 음(−)의 영향을 미치는 것으로 나타났다. 호황국면에서 금리의 영향은 불황국면에서와 같이 양(+)의 부호를 가지며, 통계적 유의성은 없는 것으로 분석되었다. 전해정(2017)의 실증 분석 기간은 2002년 5월부터 2015년 12월까지이다.
단일방정식을 사용한 해외 연구로는 Hall et al.(1997), Nneji et al.(2013), Rangel and Ng (2017)가 있다. Hall et al.(1997)은 주택가격에 대한 단일방정식 오차수정모형에 마르코프 국면전환 모형을 적용하였으며, 설명변수로는 소득, 주택 스톡, 이자율(주택대출금리) 등을 사용하였다. 1966년부터 1995년까지의 영국의 분기 데이터를 이용한 추정결과, 이자율이 주택가격에 미치는 영향은 변동성이 높은 국면에서는 음(−)의 부호를, 그리고 변동성이 낮은 국면에서는 양(+)의 부호를 가지나, 두 경우 모두 통계적 유의성은 낮은 것으로 나타났다.
Nneji et al.(2013)과 Rangel and Ng(2017)는 주택가격 방정식에 3-국면 국면전환모형을 적용하였다.10)Nneji et al.(2013)은 회귀식의 설명변수로 이자율(T-bill), 금리차, 물가, 소득을 사용하였으며, 1960년부터 2011년까지의 미국의 분기 자료를 이용한 추정결과, 이자율 상승이 3-국면 모두에서 주택가격 하락요인으로 작용하는 것으로 나타났다. Rangel and Ng(2017)는 설명변수로 물가, 환율, 인구, 공공주택공급, 실질소득, 이자율(우대대출금리)을 사용하였다. 1978년부터 2012년까지의 싱가포르의 분기 자료를 이용한 모형 추정결과, 호황국면에서는 이자율 상승이 주택가격 하락요인으로 작용하나, 다른 두 국면에서는 주택가격 상승요인으로 작용하는 것으로 분석되었다.
MS-VAR 모형을 사용한 해외 연구로는 Chang et al.(2011), Chowdhury and Maclennan(2014), Simo-Kengne et al.(2013)가 있다. Chang et al. (2011)은 이자율(연방기금금리), 주택가격, 이자율 스프레드의 세 가지 변수로 구성된 MS-VAR 모형의 충격반응함수 분석을 통해 이자율변동 효과를 살펴보았다. 1975년부터 2008년까지의 미국 데이터를 이용한 분석결과는 이자율 충격이 주택가격에 음(−)의 영향을 미치며, 효과의 크기는 단기적으로는 변동성이 낮은 국면보다는 변동성이 높은 국면에서 크게 나타나나, 장기적으로는 변동성이 낮은 국면에서의 효과가 크다는 결과를 보고하였다. Simo-Kengne et al.(2013)은 실질 주택가격과 이자율(T-bill)의 두 변수로 구성된 MS-VAR 모형을 구축하고, 1966년부터 2011년까지의 남아공의 월간 데이터를 이용하여 실증 분석하였다. 충격반응함수 분석결과는 이자율이 주택가격에 미치는 영향이 고변동성 국면에서 단기적으로 이론과는 달리 양(+)의 부호가 나타날 수 있으며, 주택가격에 미치는 이자율 충격의 효과는 고변동성 국면에서 큰 것으로 나타났다. Chowdhuriy and Maclennan(2014)은 이자율(T-bill), 실질 주택가격, 주택담보 대출, GDP의 네 변수 MS-VAR 모형을 통해 영국에서의 이자율변동 효과를 살펴보았다. 데이터 기간은 1980년부터 2012년까지이다. 이자율변동 효과는 두 국면 모두에서 주택가격에 음(−)의 영향을 미치나, 저변동성 국면에서 단기적으로 양(+)의 영향이 나타날 수 있으며, 효과의 크기는 저변동성 국면에서 크게 나타나고 있다. 충격반응함수 분석결과를 보면, 1%포인트의 이자율 인하는 주택가격을 저변동성 국면에서는 최대 0.59% 그리고 고변동성 국면에서는 최대 0.45% 상승시키는 효과가 있다(<표 1> 참조).
| Chang et al. (2011) | Simo-Kengne et al. (2013) | Chowdhury and Maclennan(2014) | |
|---|---|---|---|
| 대상국가 | 미국 | 남아공 | 영국 |
| 분석기간 | 1975~2008 | 1966~2011 | 1980~2012 |
| 평균 주택 가격증가율 | H>L | L>H | H>L |
| 평균 국면 지속기간 | L>H | H>L | L>H |
| 이자율과 주택가격 | 마이너스 | 마이너스 (H에서 단기적으로 +) | 마이너스 (L에서 단기적으로 +) |
| 이자율 충격의 효과 | H>L (단기) L>H (장기) | H>L | L>H |
Ⅲ. 분석방법
이자율이 주택시장에 미치는 영향을 실증 분석하기 위해 본 연구에서는 MS-VAR 모형을 사용한다. MS-VAR 모형은 VAR 모형에 마르코프 국면전환 모형을 적용한 모형으로, 일반적인 VAR 모형과는 달리 모수(parameter) 값들이 국면에 따라 달라지는 가변성을 가지며,11) 이에 따라 이자율이 주택시장에 미치는 영향도 국면별로 상이하게 나타날 수 있다. 본 연구의 MS-VAR 모형은 다음과 같다.
위에서 yt는 주택가격, 주택거래량, 이자율로 구성된 3×1 벡터, B0는 3×1 상수항 벡터, 나머지 Bi는 3×3 계수행렬이며, ut는 3×1 오차항 벡터이다. 오차항 벡터 ut는 0의 평균과 Σ의 공분산을 가지며, 시점 간에 독립적인 다변량 정규분포(NID)를 따르는 것으로 가정한다. 모형의 계수(Bi)와 오차항의 공분산(Σ)은 국면(St)에 따라 다른 값을 갖는다. 본 연구에서 국면의 수는 2로 설정하였다.
St는 국면을 표시하는 확률변수로서 마르코프 특성12)을 가지며, 아래와 같은 P의 전이 행렬(transition matrix)을 갖는다.
위에서 pij는 국면이 현재의 i국면에서 다음 기에 j국면으로 전이될 확률, 즉 pij=Pr(St+1=j | St=i)이다. 본 연구에서와 같은 2-국면 모형에서는 p11+p12=1, p21+p22=1이다.
MS-VAR 모형의 추정은 베이즈 정리를 적용한 최우추정법(MLE)을 사용한다. 최우 추정을 위한 우도 함수는 조건부 함수의 형태로 표시되는데, 대수우도함수(log likelihood function; L(θ))는 다음과 같다.
<식 4>에서 f(yt|θ, Φt=1)는 정규분포의 확률밀도함수이며, θ는 추정할 모형의 모수들(Bi, Σ)을 그리고 Φt–1은 t–1 시점까지의 데이터 정보 집합({yt–1, yt–2, …})을 표시한다. <식 5>는 yt의 확률밀도함수를 국면별 확률밀도함수의 합으로 표시한 것이다. 앞의 <식 1>에서 yt는 t기의 국면(st)에만 의존하나, 마르코프 속성에 따라 <식 5>에서 yt의 발생확률은 당기의 국면(st)와 전기의 국면(st–1)의 두 개 국면에 의존하는 조건부 값을 갖는다. <식 6>은 결합확률을 조건부 확률과 한계 확률(전이확률)로 분해한 것이며, 전이확률 pij는 추정되어야 할 모수이다.
<식 6>에서 Pr(st–1=i|Φt–1)는 t–1 시점의 국면이 i 국면일 확률로서 t–1 시점까지의 데이터를 이용하여 얻을 수 있는 여과확률(filtered probability)이다. 여과확률의 시계열 값은 베이지안 기법을 이용한 예측(prediction)-갱신(update)의 반복을 통해 모수 추정과정에서 구하게 된다. 추정과정에서 얻어진 여과확률을 이용하여 다음과 같은 평활화 확률(smoothed probability)을 구할 수 있다.
평활화 확률-Pr(st=i|ΦT)-은 t시점까지의 자료만을 사용하여 추정한 여과확률과는 달리 T 시점까지의 데이터, 즉 전체 표본을 통해 얻을 수 있는 국면 확률로서 국면 판단의 자료로 사용된다.
MS-VAR 모형의 추정으로 얻어진 국면별 VAR 계수와 오차항의 공분산을 이용하면 국면별 충격 반응함수를 구할 수 있다. 충격 반응함수를 구하기 위해 사전적으로 필요한 작업은 충격의 식별(identification)이다. 충격은 VAR 모형에서 변수들의 동적 움직임을 초래하는 기본적인 요인 변수로서, 본 연구에서는 이자율 충격, 주택가격 충격, 주택거래량 충격의 세 가지 충격을 고려한다.
충격 변수들로 구성된 충격항 벡터를 et라고 할 때, et는 <식 1>의 오차항 벡터 ut와 다음과 같은 선형 관계로 연결되어 있다고 가정한다.
위에서 H(St)는 3×3 계수행렬로서, 충격이 ut를 거쳐 내생변수 벡터 yt에 미치는 t시점에서의 변동효과(∂yt/∂et)를 나타낸다. H(st)는 국면별로 다른 값을 갖는다. 계수행렬 H(st)를 식별하기 위해 본 연구에서는 Pesaran and Shin (1998)의 일반화 충격반응함수를 이용하였다.13)
국면별 충격반응함수의 신뢰구간은 MCMC (Markov Chain Monte Carlo) 방법의 하나인 깁스 샘플링(Gibbs sampling)을 이용하여 계산한다. MS-VAR 모형에서의 깁스 샘플링은 다음과 같은 세 가지 과정의 표본추출을 반복하면서 모수들에 대한 표본 값들을 추출한다.
-
과정 ① 주어진 모형의 모수 값 및 전환행렬 모수를 이용하여 국면변수의 시계열 값들을 추출한다.
-
과정 ② 주어진 국면 값들을 이용하여 전환행렬을 추출한다.
-
과정 ③ 주어진 국면 값들을 이용하여 모형의 모수 값들을 추출한다.
과정 ①과 ②는 MS-VAR 모형의 여과확률과 전환행렬이 추정되어야 할 모수이기 때문에 이루어지는 작업으로, VAR 모형의 경우에는 필요치 않은 과정들이다. 본 연구에서 과정 ①의 표본추출은 Chib(1996)의 FFBS(forward filter-backward sampling) 방식을 사용하여 추출하였으며, 과정 ②의 표본추출은 디리클레(Dirichlet) 분포를 이용하였다. 과정 ③에서 모형의 모수들은 <식 1>과 <식 2>의 국면별 VAR 계수(Bi)들과 오차항의 공분산행렬(Σ)이다. B와 Σ는 동시에 추출할 수 없으며, 역위샤트(inverse Wishart) 분포로부터 Σ를 먼저 추출하고 난 후, 추출된 Σ를 이용하여 정규분포로부터 Bi를 추출하였다.
Ⅳ. 실증 분석
본 연구에서 사용하는 변수는 실질 주택가격, 주택거래량, 이자율이다. 주택가격과 주택거래량 데이터는 한국감정원에서 발표하는 아파트 실거래가격지수와 아파트매매 거래량이며, 주택가격은 소비자물가지수를 이용하여 실질 변수화하였다. 아파트가격지수는 한국감정원에서 발표되는 계절 조정치를 사용하였고, 아파트매매 거래량과 소비자물가지수는 X12-ARIMA로 계절 조정하여 사용하였다. 이자율은 주택시장과 관련성이 높은 주택담보대출금리를 사용하였다. 데이터 기간은 아파트 실거래가격지수가 발표되기 시작한 2006년 1월부터 2020년 3월까지이다.
| 수준변수 | 차분변수 | |||||
|---|---|---|---|---|---|---|
| ADF | PP | KPSS | ADF | PP | KPSS | |
| 주택가격(hp) | −1.855 | −1.959 | 1.576*** | −4.519*** | −5.857*** | 0.089 |
| 주택거래량(hq) | −3.721*** | −7.691*** | 0.123 | − | − | − |
| 이자율(i) | −0.664 | −0.642 | 2.867*** | −6.091*** | −11.174*** | 0.067 |
<표 2>는 데이터의 안정성 여부를 확인하기 위해 시행한 단위근 검정결과이다. 단위근 검정은 ADF 검정, PP 검정, KPSS 검정을 사용하였으며, 검정식에서 추세(trend) 항은 고려하지 않았고 차수(lag)는 6으로 설정하였다. <표 2>의 검정결과에서 보는 바와 같이 주택가격과 이자율은 I(1)으로 그리고 주택거래량은 I(0)으로 검정되며, 이 결과에 따라 주택가격과 이자율은 차분하여 사용하고 주택거래량은 수준변수를 그대로 사용하였다. <표 3>은 본 연구에서 사용되는 변수에 대한 기초통계량으로, Δhp는 주택가격증가율, hq는 로그변환된 주택거래량, Δi는 차분된 이자율을 나타낸다.
먼저, MS-VAR 모형의 타당성을 검토하기 위해 VAR 모형과의 우도비 검정을 시행하였다. <표 4>는 우도비 검정결과이다. 우도비 검정은 χ2 분포를 이용하며, 모형의 차수(lag)는 1-4를 고려하였다. 표에서 보는 바와 같이, 검정통계량(우도비)은 모두 차수에 상관없이 1% 유의수준에서 기각되면서 MS-VAR 모형이 통상적인 VAR 모형보다 통계적으로 적정함을 보여주고 있다.
| 평균 | 분산 | 왜도 | 첨도 | JB | |
|---|---|---|---|---|---|
| Δhp | 0.158 | 0.659 | 0.998*** | 10.6*** | 830.4*** |
| hq | 1,083.6 | 812.6 | −0.458** | 1.636*** | 25.0*** |
| Δi | −0.017 | 0.025 | −2.056 | 15.7*** | 2,450.5*** |
<표 5>는 MS-VAR 모형에 대한 추정결과이다. 모형의 추정을 위해서는 먼저 모형의 차수가 결정되어야 한다. 모형의 차수는 AIC와 BIC 모두에서 적정 차수로 계산된 1로 설정하였다. <표 5>에서 국면 A, B의 구분은 주택가격 방정식 오차항의 분산 크기에 따라 구분하였으며, 국면 A는 오차항의 분산이 작은 국면을 그리고 국면 B는 오차항의 분산이 큰 국면을 표시한다.
모형 추정결과에서 주목할 만한 결과는 네 가지이다. 첫째, 주택가격의 변동성이 높은 국면 B에서 주택거래량과 이자율 역시 변동성이 높게 나타나고 있다. 이러한 결과는 주택시장에서 가격과 거래량의 변동성이 연계되어 있으며, 주택시장과 이자율의 관계에서도 변동성이 상호 관련성이 있음을 시사한다. 둘째, 국면별 변수 평균14)에서는 주택가격의 경우 고변동성 국면에서의 월평균 상승률이 0.965%로 저변동성 국면의 0.168%보다 압도적으로 높은 수치를 보인다.15) 이자율의 경우에는 고변동성 국면에서 이자율의 월평균 하락 폭이 컸으며, 주택거래량(hqt)의 경우에는 국면별 평균 차이가 두드러지지 않았다. 셋째, 국면의 평균 지속기간은 저변동성 국면이 압도적으로 길었다.16) 저변동성 국면이 지속할 확률(P11)과 고변동성 국면이 지속할 확률(P22)은 각각 0.922와 0.637이며, 이러한 전이확률에서 계산되는 각 국면의 평균 지속기간은 12.9개월과 2.8개월이다.17) 넷째, 이자율이 주택시장에 미치는 영향 혹은 주택시장의 변화가 이자율에 미치는 영향과 관련하여, 계수 추정값의 크기(절댓값)는 고변동성 국면에서 큰 값을 갖는다. 이러한 결과는 주택시장과 이자율 상호 간의 영향력이 고변동성 국면에서 상대적으로 높게 나타날 수 있음을 의미한다. 다섯째, 주택가격 방정식에서 주택거래량의 계수 그리고 주택거래량 방정식에서 주택가격의 계수는 두 국면 모두에서 양(+)의 값을 보인다. 이러한 양(+)의 관계는 이자율 충격의 효과가 주택시장 내에서 주택가격과 주택거래량의 상호작용을 통해 확대될 수 있음을 의미한다.
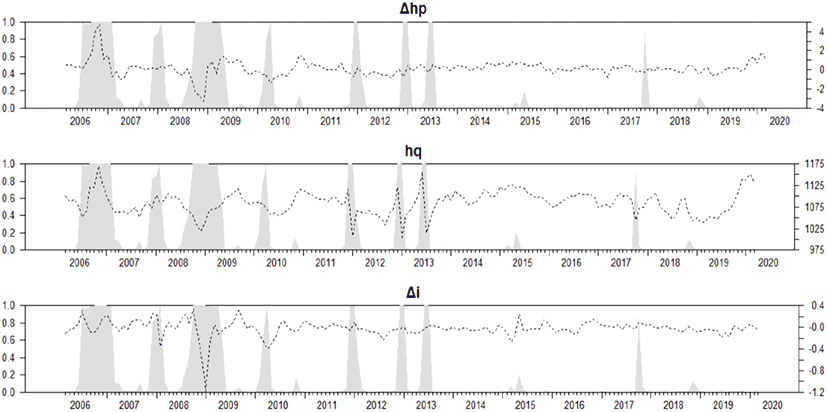
<그림 1>은 평활화 확률 추이로서 고변동성 국면이 나타날 확률을 표시한다. 그림에서 보는 것처럼, 금융위기 기간을 전후하여 고변동성 국면이 두드러지게 나타났으며, 2010년 이후에는 고변동성 국면이 간헐적으로 나타나고 있다. 고변동성 국면에서는 변수들의 증가율(폭)뿐만 아니라, 감소율(폭)도 높다. 이러한 결과는 <표 4>의 모형 추정결과에서 나타난 주택가격의 고변동성-고가격증가율(평균)의 관계가 고위험-고수익의 관계가 아니라, 단순히 고변동성 기간에 주택가격 급락 현상보다는 주택가격 급등 현상이 상대적으로 많았다는 것으로 해석해야 함을 의미한다.
이 절에서는 충격 반응함수와 예측오차 분산분해 결과를 통해 금리 변동이 주택시장에 미치는 효과가 국면에 따라 어떻게 다른지 살펴본다.
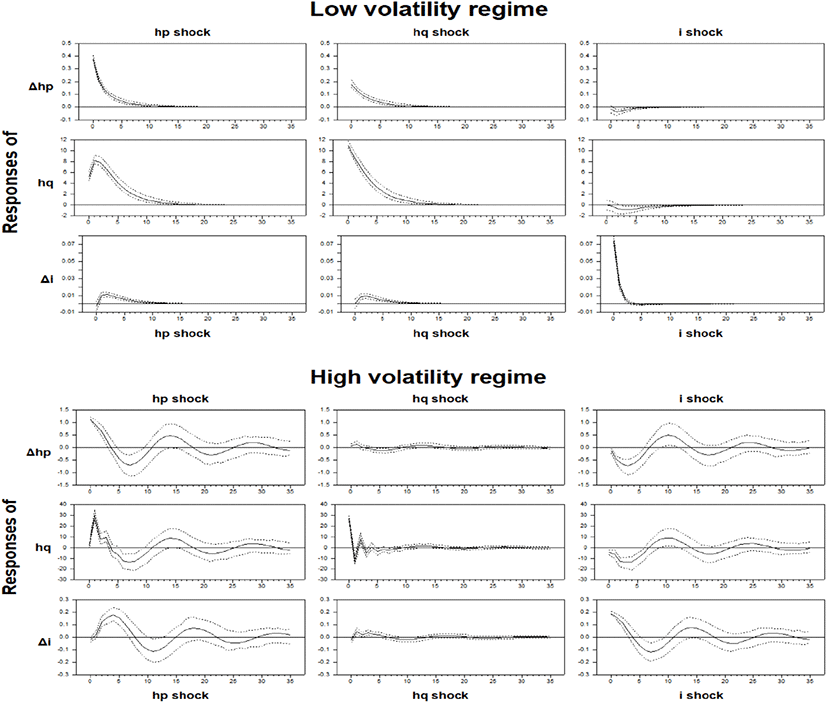
<그림 2>는 각 충격에 따른 변수들의 충격 반응함수로서, 해당 국면의 해당 방정식에서 1단위 표준편차의 충격이 발생하였을 경우의 충격 반응함수이다. Ⅲ장에서 언급한 바와 같이 본 연구에서 충격은 이자율 충격, 주택가격 충격, 주택거래량 충격의 세 가지이다. 그림에서 보는 것처럼 저변동성 국면과 고변동성 국면에서의 충격 반응함수의 형태는 크게 다르다. 먼저 저변동성 국면의 경우, 이자율 충격이 주택시장에 미치는 효과 그리고 주택시장에서의 가격이나 거래량 충격이 이자율에 미치는 효과는 경제이론에서 이야기되는 바와 같다. 즉 이자율 상승은 주택가격 및 주택거래량의 위축을 가져오며, 주택시장에서의 호황(주택가격과 주택거래량의 증가)은 이자율(주택담보대출금리)의 상승을 초래하고 있다. 고변동성 국면에서도 충격에 따른 변수들의 반응은 대체로 저변동성 국면에서와 비슷한 방향으로 이루어지고 있다. 그러나 충격에 따른 반응의 정도가 고변동성 국면에서 훨씬 크고, 오랫동안 충격 효과가 지속하며, 변수에의 영향이 지그재그로 바뀌면서 변수의 변동성이 커진다는 점에서 두 국면 간에는 커다란 차이가 존재한다.
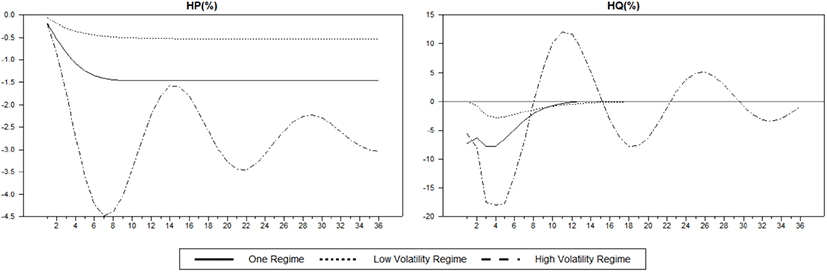
<그림 3>은 이자율이 0.25%p 상승하는 경우에 나타나는 주택시장에서의 충격 반응함수를 비교하고 있다.18) 비교는 VAR 모형, 그리고 MS-VAR 모형에서의 두 개 국면을 대상으로 하였으며, 이자율 충격이 주택시장의 수준변수에 미치는 영향을 살펴보기 위해 주택가격의 반응은 누적 충격치로 환산하였다.19) 그림에서 보는 바와 같이, VAR 모형에서의 충격 반응함수와 저변동성 국면에서의 충격 반응함수는 절대적인 크기를 제외하면 전체적으로 비슷한 형태를 보이나, 고변동성 국면에서의 형태는 이들 둘과는 큰 차이를 보인다. MS-VAR 모형에서 두 국면 사이의 충격 효과의 크기를 수치로써 비교하면, 우선 저변동성 국면에서는 0.25%p의 이자율 상승충격이 주택가격을 0.53%까지 하락시키며, 주택거래량은 4개월 후 2.81%까지 하락하였다가 점차 원래 수준으로 회복되고 있다. 고변동성 국면의 경우에는 이자율 0.25%p의 상승충격이 주택가격을 최대 4.48%까지 그리고 주택거래량은 최대 17.98%까지 하락시킨다. 이러한 결과는 같은 크기의 이자율 충격이 미치는 주택시장에의 파급효과가 고변동성 국면에서 압도적으로 크게 나타나고 있음을 보여준다.
<표 6>은 예측 오차 분산분해 결과이다. 이자율 충격이 주택시장 변수의 변동에서 차지하는 비중은 고변동성 국면에서 압도적으로 크게 나타나고 있다. 고변동성 국면에서 이자율 충격이 차지하는 비중은 예측 시계 ∞에서 주택가격증가율 변동의 37.01% 그리고 주택거래량 변동의 28.13%인 반면에, 저변동성 국면에서는 그 비중이 1.27%와 0.49%로 매우 작다. 한편, 주택시장 충격이 이자율변동에 미치는 영향 면에서는 주택가격충격의 비중이 주택거래량 충격의 비중보다 높으며, 특히 고변동성 국면에서는 주택가격 충격의 비중이 52.75%에 달하고 있다.
Ⅴ. 맺는 글
본 연구에서는 MS-VAR 모형을 이용하여 이자율변동이 주택시장에 미치는 동태적 영향이 국면별로 어떻게 다른가를 살펴보았다. 국면은 고변동성 국면과 저변동성 국면의 두 가지로 구분하였다. 모형에서 사용한 변수는 실질 주택가격, 주택거래량, 이자율(주택담보대출금리)의 세 변수이며, 충격은 이자율 충격, 주택가격충격, 주택거래량 충격의 세 가지이다. 충격의 식별은 Pesaran and Shin(1998)의 일반화 충격 반응함수를 이용하였다. 모형의 추정은 최우 추정법을 사용하였으며, 데이터 기간은 2006년 1월부터 2020년 3월까지이다. 이자율변동이 주택시장에 미치는 동태적 파급효과는 충격 반응함수와 분산분해 분석을 이용하여 분석하였으며, 분석의 현실감을 높이기 위해 이자율 충격의 크기는 통화정책의 기준금리 조정 기본단위인 0.25%p로 설정하였다.
분석결과를 정리하면 다음과 같다. 첫째, 우도비 검정결과는 단일국면 VAR 모형보다 2-국면 MS-VAR 모형이 통계적으로 적절함을 보여준다. 이러한 검정결과는 주택시장에 미치는 이자율변동의 파급효과가 국면에 따라 다르게 비대칭적으로 나타난다는 것을 의미한다. 둘째, 고변동성 국면보다는 저변동성 국면이 일반적이며 평균 지속기간도 길었다. 다만, 이러한 결과는 분석 기간에 따라 달라질 수 있다는 점에 주의할 필요가 있다. 셋째, 고변동성 국면에서는 주택가격 증가율의 평균이 높고 이자율 하락 폭의 평균도 컸으나, 거래량은 고변동성 국면과 저변동성 국면에서 별 차이가 없었다. 고변동성 국면에서 주택가격 증가율의 평균이 높았던 것은 우리나라의 경우 주택가격 급락보다는 주택가격 급등이 더욱 빈번하게 발생하였기 때문이며, 고위험-고수익 혹은 고변동-호황의 관계로 해석하는 것은 무리가 있다.20) 셋째, 이자율변동이 주택시장에 미치는 영향은 고변동성 국면에서 훨씬 크게 나타났다. 0.25%p의 이자율 상승충격이, 저변동성 국면에서는 주택가격을 0.53%까지 그리고 주택거래량을 2.81%까지 하락시키며, 고변동성 국면에서는 주택가격을 4.48%까지 그리고 주택거래량을 17.98%까지 하락시키는 효과가 있다.21) 본 연구의 분석결과에서 나타난 여러 가지 국면별 차이는 주택시장에 영향을 주는 경제정책 수립 시 좀 더 세심한 국면 점검과 정확한 국면별 정책 파급효과 파악이 선행되어야 함을 시사하고 있다.
본 연구에서는 통상적으로 사용되는 MS-VAR 모형에서의 국면 구분 방식을 그대로 원용하였다. MS-VAR 모형에서의 통상적인 국면 구분은 변동성의 크기에 따라 이루어진다. 여러 개의 변수가 사용될 경우 변동성에 입각한 국면 구별이 정확히 무엇을 의미하는지 해석하기 어려울 수 있다. 또한, 여러 변수를 포함한 모형에서의 변동성 국면이 개별 변수에서 계산되는 변동성 국면과 차이를 보일 수도 있으며, 국면 구분을 변동성이 아닌 다른 방식, 예컨대 상승국면과 하강국면으로 구분하여 분석할 필요도 있다.22) 따라서 MS-VAR 모형을 이용한 분석이 좀 더 현실적인 분석이 되기 위해서는 다양한 국면 구분을 담아낼 수 있는 다각도의 모형 개발이 필요할 것이다.