Ⅰ. 서론
주택시장의 모든 가격 정보를 하나의 숫자로 표현할 수 있는가? 주택시장을 나타내는 대표적인 숫자로는 가격지수를 들 수 있다. 시장을 적절히 대표하는 가격지수가 가지는 장점은, 시장에 존재하는 수많은 정보를 하나의 숫자로 압축함으로써 거시적 관점에서 시장을 바라보고 분석할 수 있게 한다는 점이다. 이로 인해 주택시장에 대한 대부분의 논의는 가격지수를 중심으로 이루어진다. 하지만 일각에서는 가격지수가 나타내는 시장과 실제로 체감하는 시장 간 괴리가 존재한다는 반응도 존재한다. 지수와 현실 간 괴리에 대하여는 호가·실거래가의 차이, 표본 구성의 문제 등의 여러 이유가 있을 수 있겠지만(이용만, 2007), 본 연구에서는 지수가 제공하지 못하는 정보를 시장 참여자들이 체감하면서 일부 괴리가 발생할 가능성에 주목하고자 한다. 이러한 잠재적 간극을 좁히기 위해, 지수가 산출되는 주택시장의 패널데이터를 구축하여 가격 변화의 분포를 구축하고, 기존 지수가 가지는 설명력을 보완할 수 있는 분포의 특성들을 살펴본다.
지수가 가지는 특징이자 장점은 시장에 존재하는 모든 정보를 숫자 하나로 압축한다는 점이지만, 동시에 이로 인해 지수가 살피지 못하는 맹점이 발생한다. 지수란 본질적으로 분포의 형태로 존재하는 전체 정보를 가장 적절하게 대표할 수 있는 숫자를 의미한다. 따라서 평균적인 가격, 평균적인 움직임을 나타내도록 설계되는데, 이 과정에서 분포상 평균보다 높거나 아래에 있는 시장의 정보들은 소실된다. 분포가 넓게 펴져 있어 평균적으로는 가격이 상승하지만 개별적으로는 가격이 하락한 주택이 적지 않게 존재한다면, 해당 가구들은 지수의 상승폭만으로 시장을 설명할 때 자신들이 체감하는 현실과 괴리를 느낄 것이다. 또한, 주택가격에 기반한 유한책임대출을 공급하는 금융기관 입장에서는 평균적인 가격의 움직임이 아닌, 실제로 손실이 발생할 수 있는 수준의 가격하락 폭이 발생할 가능성 및 비중이 더 중요한 정보일 것이다.
이런 잠재적 한계에도 불구하고 주택시장을 지수로 요약하는 것이 적절한지 알기 위해서는 주택시장의 전체 가격 분포를 살펴봐야 한다. 분포가 정규분포에 가깝거나, 정규분포는 아니지만 충분히 좌우대칭이며 좁게 분포한다면, 지수라는 숫자 하나로 대표하더라도 시장의 전체적인 움직임을 살핀다는 측면에서는 큰 무리가 없을 것이다. 하지만 분포의 모습이 쌍봉의 모습을 보이는 등, 일반적인 분포의 모습이 아니라면 숫자 하나만으로는 표현하기 적절하지 않을 수 있다.
이를 통해 이 연구에서 보고자 하는 것은 첫째, 주택가격 변화율 분포의 일반적인 특성이다. 분포의 평균, 표준편차, 왜도, 첨도 등의 모멘트들과 그래프의 모양을 통해 분포의 특성을 파악하고 주택가격 변화율 분포가 하나의 숫자로 적절하게 설명될 수 있는지를 살핀다.
둘째, 가격지수가 상승할 때와 하락할 때를 구분하여 가격 분포를 살펴본다. Ⅱ장에서 다시 살펴보겠지만, Ohnishi et al.(2020)은 도쿄의 주택가격 분포가 크기에 대하여 보정하면 로그정규분포를 따르지만, 버블 시기에는 로그정규분포보다 꼬리가 두터운 형태를 따른다는 것을 밝혔다. 이는 주택가격 상승기에는 주택가격 변화율 분포가 다른 때와는 다른 모습을 지닐 수 있다는 것을 의미한다. 금융기관이 스트레스 테스트를 실시할 때는 시나리오별로 충격의 크기를 산출하게 되는데(European Central Bank, 2021; Gross, et al., 2020), 만약에 주택가격 상승기와 하락기 간 차이를 고려하지 않고 평균적인 움직임을 가정한다면 위험을 과소평가할 가능성이 있다. 이에 주택가격지수 변화율 수준별로 주택가격 변화율 분포를 각각 계산해 주택가격 상승기와 하락기에 분포의 특성이 어떻게 달라지는지 파악한다.
마지막으로, 전체 평균과 다른 움직임을 보이는 주택들의 특성에 대해 알아본다. 주택가격지수가 시장의 전체적인 움직임을 잘 반영하더라도, 시장 참여자들의 주목도가 높은 특성을 가진 주택들이 가격지수보다 크게 오르거나 내린다면 시장 참여자들은 가격지수와 현실 간 괴리가 존재한다고 인식할 가능성이 있다. 주택의 지역, 크기, 가격대별로 분포를 구하고, 클러스터링 기법을 통해 분포의 모습이 비슷한 주택 특성별로 묶어 전체 평균과 다른 움직임을 보이는 주택들에 대해 알아본다.
Ⅱ. 선행연구
주택시장의 가격 분포를 살펴본 연구는 그 수가 많지 않은데, 주택시장의 분포를 처음으로 다룬 연구들은 주택가격 분포와 소득 분포 간 관계에 주목하였다(Gyourko et al., 2013; Määttänen and Terviö, 2014; Van Nieuwerburgh and Weill, 2010). 이들은 주로 소득의 불균형 심화가 주택 가격 차이의 심화로 이어지는지를 다루었다.
주택가격 분포 자체에 관심을 가진 대표적인 연구로는 McMillen(2008)을 꼽을 수 있다. 이 연구는 시간에 따른 주택가격 분포 모양의 변화가 주택의 크기나 위치 등의 속성의 변화에 의한 것이 아니라, 주택가격 분위별 주택가격을 설명하는 회귀식의 변화에 의한 것임을 밝혔다.
Ohnishi et al.(2020)은 도쿄의 주택가격 분포를 분석하였다. 이들에 따르면 주택가격 분포 로그정규분포보다 꼬리가 더 두터운 형태이며, 특히 꼬리는 파워-로 분포(power law distribution)표현될 수 있다. 또한, 주택규모에 따른 가격 차이를 크기로 보정한 분포는 표본기간 대부분에서 이론과 부합하게 로그정규분포를 따르지만, 버블 시기에는 로그정규분포보다 꼬리가 더 두터운 형태를 나타낸다는 것을 밝혔다. 이들은 이를 바탕으로 주택가격 분포의 모양을 통해 버블을 진단할 수 있는 가능성을 제시하였다.
이러한 연구들은 주택가격의 횡단면적 분포를 다루었는데, 이것만으로는 가격지수의 적절성을 따지기 어렵다. 가격지수란 현재의 가격 수준 자체를 보는 것이 아니라, 특정 시점을 기준으로 정규화된 가격 수준을 보는 것으로, 가격의 변화율이 핵심적인 정보이다. 하지만 선행연구에서 사용한 주택가격 횡단면 데이터만으로는 가격의 변화율 분포를 분석하지 못한다. McMillen(2008)은 1995년과 2005년 각각에 대하여 주택가격을 설명하는 회귀식을 추정하였으므로 전반적인 가격 수준의 변화율은 상수항의 변화로 나타나게 되는데, 회귀식을 각 가격분위(25%, 50%, 75%)에 대해 추정하여 각 주택가격 분위별 가격 변화율을 다루게 된다. Ohnishi et al.(2020)도 마찬가지로 연도별로 주택가격을 정규화한 후 분위별 가격수준을 기초로 논의를 전개한다. 이렇듯 횡단면의 정보만을 가지고 주택가격 변화율의 분포를 살피고자 할 때의 문제는, 각 분위별 가격 상승률이 동일하더라도 실제 주택가격 변화율의 분포는 다를 수 있다는 점이다. 예를 들어, 50% 가격 수준이 100이고 60% 가격 수준이 110이었는데 3년 후에 50% 가격 수준은 110이 되고 60% 가격 수준은 120이 된 경우를 가정해 보자. 이 경우에, 가격이 100, 110이었던 주택이 3년 후 110, 120이 된 경우가 있을 수 있는 반면, 가격이 100이었던 주택이 120으로 오르는 동안 110이었던 주택이 110에 머물러 있을 가능성 또한 존재한다. 전자의 경우 각 주택의 가격 변화율은 10%, 9.1%인 반면 후자의 경우 20%, 0%로 가격 변화율의 분포는 전혀 다른 모습을 보일 수 있다. 즉, 주택가격의 횡단면적 분포만으로는 주택가격 변화율 분포를 알 수 없으므로 주택가격지수가 주택가격 변화율을 적절히 대표하고 있는지 알 수 없다는 것이다.
이를 해결하기 위해 이 연구에서는 이러한 한계를 극복하기 위해 김경외·정성도(2017), 류강민·이상영(2010), 민병철(2021), 이영수·심소임(2016)에서 활용한 방법을 따라, 아파트 특성이 동일한 주택을 동일주택으로 간주하여 주택가격의 패널 데이터를 구축하고 주택가격의 변화율 분포를 분석하였다. 류강민·이상영(2010)과 이영수·심소임(2016)은 아파트 단지명, 면적, 평형타입이 같은 경우를, 김경외·정성도(2017)는 아파트 단지명, 면적이 같은 경우를, 민병철(2021)은 단지명, 면적, 층수(2층 이하/초과)가 같은 경우를 동일주택으로 보았다. 본 연구에서는 일반적으로 저층의 주택가격이 낮다는 점을 고려하여 민병철(2021)의 방식을 따라 패널데이터를 구축하였다.
이 연구의 의의는 최초로 주택가격의 변동성 분포를 주택가격의 패널데이터를 통해 분석하였다는 점에 있다. 해외에서는 주택가격의 횡단면 분포를 분석한 연구는 존재하였으나 패널데이터를 이용한 주택가격 변동률 분포를 다룬 연구는 아직 발견하지 못하였다. 이는 주택의 거래가 빈번하지 않아 시계열 정보를 만들기 어려운 한계에 일부 기인한 것으로 보인다. 한국은 아파트의 거래비중이 높다는 점과, 아파트는 속성과 가격이 유사한 세대가 많다는 점을 이용하여 주택가격의 패널데이터를 구축하기에 유리한 환경을 갖추고 있다. 국내선행 연구들은 이를 활용해 주로 Shiller(1991)가 제안한 반복매매모형을 통해 패널테이터 기반 가격지수를 계산하였다. 류강민·이상영(2010)은 부동산114의 시세자료를 이용하여 가치가중 반복매매지수 산정방법으로 주택가격지수를 계산하였다. 이들은 주택 투자의 관점에서는 당시 국토해양부가 채택한 동일가중 반복매매모형보다 가치가중 반복매매지수가 보다 의미 있는 지표가 될 수 있다고 제안하였다. 김경외·정성도(2017)는 2011년 7월부터 2016년 6월까지의 서울시 아파트 매매 실거래 데이터를 이용하여 실거래 가격지수를 계산하였다. 하지만 이들 연구는 패널데이터를 통해 가격지수를 계산하였지만 패널데이터가 나타내는 가격 변화율 분포에 대하여는 다루지 않았다.
또한, 이 연구의 분석결과는 추후 유한책임대출의 위험관리에도 활용이 가능하다. 유한책임대출은 주택가격이 대출잔액 이하로 떨어져 차추가 전략적으로 부도를 선언할 경우, 금융기관이 대출잔액과 주택가격의 차이만큼 손실을 입게 되는 대출이다. 이는 민병철(2021)에서 다룬 역전세 위험과 마찬가지로, 주택가격 변화율이 일정 수준 이상일 때부터 위험이 급격하게 증가하기 때문에 가격지수의 움직임만으로 위험을 추정 시 과소평가할 우려가 있다. 김종희(2017)는 주택담보대출의 대손율을 추정하는 연구를 하였는데, 정상상태에서 대손율과 금리, 경제 상황, 그리고 가격 간 선형 관계를 추정하고 이를 이용해 충격 상태에서의 대손율을 추정하였다. 본 연구에서와 같이 주택가격 변화율 분포를 정량적으로 도출하고, 이를 토대로 주택담보대출의 잠재적 손실률을 측정한다면 주택가격의 변화에 따른 비선형적인 손실의 증가를 보다 합리적으로 추정하여 금융기관의 위험관리에 도움이 될 수 있다.
마지막으로, 이 연구에서 결과는 이론적으로 계산한 전월세전환율과 실제 세상에서 관측되는 전월세전환율 간의 간극을 일부 설명할 수 있다. 전월세전환율에는 임차인이 보증금을 돌려받지 못할 위험이 반영된다. 임대인의 부도로 인해 주택을 매각하고도 회수를 하지 못한 금액은 임차인의 손실로 이어지기 때문에, 임대인은 주택가격의 변동성을 고려하게 되고 이것이 균형가격에 반영된다. 안세륭 외(2020)에서는 임대인의 부도 리스크를 구조적 모형에 반영하여 전월세전환율을 분석하였는데, 이들이 현실과 비교하여 크게 동떨어지지 않은 모수값들을 적용하고 일반적으로 사용되는 정규분포의 가정을 사용하여 계산한 전월세전환율은, 실제 세상에서 관측되는 값보다 상당히 낮은 값을 나타내었다. 만약에 주택가격 변화율의 분포가 정규분포와 비교하여 꼬리가 두터운 형태를 띤다면, 정규분포를 이용한 경우보다 더 높은 전월세전환율을 나타낼 것이며, 이론적으로 계산한 전월세전환율보다 실제 세상의 전월세전환율이 높은 것을 일부 설명할 수 있다.
Ⅲ. 분석 방법 및 사용 자료
이 연구에서는 민병철(2021)에서 전세가격 변화율 분포를 생성하는 데 사용한 방법을 따라 주택가격 변화율 분포를 생성하였다. 이에 사용된 주 가정은, 주택의 특성이 같다면 시장에서 동일한 가격을 가질 것이라는 것이다. 이 과정에서 사용한 특성은 시군구 단위의 주소, 단지명, 건축 연도, 면적(1의 자리에서 반올림), 층수(2층 이하/초과) 등이다. 3층부터의 저층/고층 간 가격 차이나 조망 차이, 수리 상태 등에 의한 차이는 무시되었으며, 본 연구의 결과는 이로 인한 잠재적 오차에 노출되어 있다는 한계를 갖는다.
먼저 주택 특성을 통해 같은 상품에 대한 거래로 간주되는 건들을 모아 시계열 정보를 만들되, 3개월 단위로 정보를 모았다. 예를 들어, 2011년 3월의 가격 정보는 2011년 1, 2, 3월의 거래기록을 모으되, 복수의 거래정보가 존재할 경우 평균값을 사용하였다. 마찬가지로 2011년 4월의 가격은 2011년 2, 3, 4월의 거래기록을 모아 계산하였다. 이후에도 존재하는 결측치들은 내삽법을 이용하여 채우되, 최초 거래일과 최종 거래일 사이의 값들만을 채웠다(<표 1> 참조). 최초 거래일 이전은 주택이 지어지기 전이어서, 최종 거래일 이후는 주택 철거 혹은 재개발로 인해 자료가 존재하지 않았을 수 있기 때문이다. 김경외·정성도(2017) 또한 결측치들을 1차적으로 내삽법을 이용하여 채웠다. 다만, 이들은 3개월 이상의 연속된 결측치는 군집 정보를 활용한 선형회귀대체법으로 추정하였다.
동일한 단지에 대하여 복수의 단지명이 사용된 경우나, 시의 통합 및 면 단위의 읍 승격 등으로 인해 복수의 주소가 사용된 경우는 수작업으로 연결하였다.
주택가격에 대한 패널자료를 만든 후, 매매가격의 3년 변동률을 계산하였다. 2012. 6. 29. 이전에는 3년 이상 보유해야 세대 1주택에 대한 양도소득세가 부과되지 않았던 점, 그리고 본 연구의 분석대상 기간이 2006~2021년으로, 대략 절반 가까운 기간이 이에 해당한다는 점을 감안, 평균 주택 보유기간이 3년은 될 것이라고 가정하였다.
이를 토대로 계산한 매매가격의 3년 변화율에 대한 경험적 누적분포함수(empirical cumulative distribution function) F(x)는 <식 1>과 같다. 여기서 ri,j,t는 i 지역, j 아파트 단지, t 시점에 구입한 주택의 향후 3년 매매가격 변화율이며, ni,j,t는 i 지역, j 아파트 단지, t 시점의 거래량이다. I(condition) 은 condition이 참이면 1, 거짓이면 0의 값을 갖는 함수이다. <식 1>은 분석 기간 중 임의의 시점에, 분석대상 중 임의의 주택을 구입하고 3년 동안 보유했을 때 기대할 수 있는 매매가격 변화율의 분포를 의미한다.
<식 1>은 전체 표본기간에 대한 분포이므로, 주택가격 상승기와 하락기가 모두 포함되어 있다. 주택가격 변화율 분포가 주택가격 상승기와 하락기에 달라지는 모습을 보기 위해서는 매매가격지수 변화에 대한 조건부 실거래 가격 분포를 구해야 한다. 매매가격지수 분석 대상 구간의 개수를 nidx라 하고, 각 구간의 상한과 하한을 각각 라 두자. 또한, ri,t를 지역 i의 t 시점으로부터 3년간 매매가격지수 변화율이라 하자. 그러면 위에서 정의한 k번째 매매가격지수 변화율 구간에 대한 조건부 실거래 가격 분포의 누적확률분포는 <식 2>와 같이 표현된다.
예를 들어, 는 u5=0.1, l5=0.05라 할 때, 향후 3년간 매매가격지수가 5%~10% 증가하는 기준 월·지역의 표본 중 매매가격이 3년 동안 20% 이하로 상승한 비중을 뜻하며, 10% 초과 20% 이하 상승한 비중은 F5 (0.2)-F5 (0.1)로 나타낼 수 있다. 이후 편의상 <식 1>로 계산한 분포는 비조건부 분포, <식 2>로 계산한 분포는 조건부 분포라 지칭한다.
<식 2>를 따라 조건부 분포를 계산하되, 지역별, 크기별, 가격대별로 각각 계산하였다. 지역은 수도권, 5대광역시, 기타 지역으로 나누었다. 크기는 일반적인 소형/중형/대형주택의 기준을 사용하여 85m2 이하, 85~135m2, 135m2 초과로 나누었다. 1인가구라면 소형 주택을, 자녀가 있다면 중간~대형 주택을 선호하는 등, 가구의 특성별로 원하는 주택의 크기가 다를 수 있어 크기별로 나누었다. 주택가격은 과거 12개월간 해당 지역, 해당 크기 거래건 중 하위 30%(저가주택), 30%~70%(중간 가격 주택), 상위 30%(고가주택)로 나누었다. 예를 들어, 2015년 1월~2015년 12월 경기지역에서 거래된 85m2 이하의 아파트 중 거래가 기준 하위 30% 가격을 2016년 1월 경기지역의 소형·저가 주택 기준으로 사용하였다. 경기도에서는 상대적인 저가 주택일지라도 비수도권에서는 고가일 수 있으며, 반대로 비수도권에서는 고가일지라도 경기도에서는 중저가 주택일 수 있어 시도별로 저가·고가주택의 기준을 계산하였다. 또한, 2006년에는 고가 주택으로 인식될 가격이 2021년에는 중간~저가 주택으로 인식될 수 있어, 월별로 가격 기준을 달리 사용하였다. 비슷한 가구 형태 혹은 생애주기에 있어 비슷한 크기의 주택을 보유하고자 하더라도, 소득이나 자산 수준에 따라 구입하고자 하는 주택의 가격대가 다를 것이라 본다면, 가격대별로 시장 참여자들의 특성이 다를 것이므로 가격대 또한 분석의 대상으로 삼았다. 실제 계산한 가격 기준의 일부를 <표 2>에 나타내었다.
| 연월 | 서울 | 인천 | 경기 | 부산 | 대구 |
|---|---|---|---|---|---|
| 2020.11 | 4.80 | 1.85 | 2.30 | 1.97 | 1.87 |
| 2020.12 | 4.85 | 1.85 | 2.30 | 1.90 | 1.88 |
| 2021.1 | 4.96 | 1.85 | 2.30 | 1.90 | 1.87 |
| 2021.2 | 5.00 | 1.84 | 2.27 | 1.88 | 1.86 |
| 2021.3 | 5.17 | 1.80 | 2.25 | 1.86 | 1.86 |
위 과정을 통해 주택 특성별로 조건부 분포를 주택가격지수 변화율 구간별로 생성한 후, 이를 이용하여 클러스터링을 분석을 시도하였다. <식 2>를 이용하여 계산한 조건부 분포를 히스토그램의 형태로 나타내어 히스토그램 각 구간별 빈도를 변수로 사용하였다. 예를 들어, 지역 매매가격지수 변화율(−10%, 0%, 10%, 20%, 30%)에 대한 조건부 분포의 히스토그램 각 구간(개별 주택의 가격 변화율; −30%, −20%, −10%, 0, 10%, 20%, …)을 변수로 사용하였다(<표 3> 참조). 클러스터링 알고리즘으로는 계층적 군집분석 방법(hierarchical clustering)을 사용하였으며, 표본 간 거리를 측정하는 측도로는 와드 연결법(Ward linkage method)을 사용하였다. 이는 오차제곱합(error sum of square)을 최소화하는 방식이다.
본 연구에서 사용한 주 자료는 아파트 매매 실거래 정보이며, 자료 출처는 국토교통부이다. 공개되는 자료 중에서 각 거래의 가격, 단지명, 면적, 주소, 그리고 신고 일자 정보를 사용하였다. 원자료는 국토교통부 내부에서 일부 이상치를 제거한 뒤 공개하는 것으로 알려져 있다. 다만, 그 구체적인 기준은 공개하지 않는다. 자료를 패널데이터 형식으로 변환한 뒤 3년 가격 변화율이 150%를 초과하거나 −50% 이하라고 계산되는 건들은 일반적이지 않은 거래정보라 판단하고, 이상치일 가능성을 고려하여 배제하였다. 표본 기간은 2006년 1월부터 2021년 3월까지이며, 총관측 수는 8,995,086건이다.
사용한 표본의 기초통계량은 <표 4>에 나타내었다. 3월까지의 자료만을 사용한 2021년을 제외하면 454,645건이 거래된 2012년의 관측 수가 가정 적었고 856,817건이 거래된 2020년의 관측 수가 가장 많았다. 평균 거래가격은 2006년 14,619만 원에서 2021년 33,791만 원으로, 약 2.3배 뛰었다. 표본자료 중 최고가는 1,150,000만 원이었으며 최저가는 100만 원이었다.
주소·단지명·면적·층수·건축 연도가 같다면 같은 주택에 대한 거래로 간주하였는데, 이러한 주택의 숫자는 <표 5>의 두 번째 열에 나타내었다. 주택의 가격 정보가 기준 시점과 3년 후에 모두 존재하여야 가격 변동률 정보가 생성되는데, 이러한 조건을 만족하여 실제 변동률 분포에 포함된 표본 수는 세 번째 열에 나타내었다. 거래 시점 기준으로 3년 동안의 변동률을 나타내었으므로 2006~2018년에 거래된 주택의 가격 변화율 정보가 포함된다. 2019~2021년의 거래기록은 그 자체로는 가격 변화율을 분포에 포함되지 않지만, 2016~2018년에 기록된 거래 건들의 3년 가격 변화율을 계산하기 위한 가격정보를 생성하는 데 사용된다. 앞서 한 주택에 대하여 최종 거래기록 이후에 대하여는 외삽법으로 채우지 않았다고 했는데, 최근으로 넘어올수록 최종 거래일 이후인 경우가 많아져 주택 개수는 줄어든다. 예를 들어, A아파트 1~2층의 최종 매매거래일은 2016년 2월이었으며 그 이후는 거래가 발생하지 않았거나 전세 거래만 발생하였다면, 2016년 3월부터는 A아파트 1~2층의 가격정보가 생성되지 않아 총 주택 숫자에서 빠지게 된다.
조건부 분포를 만들 때 기준이 되는 매매가격지수는 전국 주택가격동향조사 아파트 매매가격지수(출처: 한국부동산원)를 사용하였다. 기간은 실거래 자료와 동일하게 2006년 1월부터 2021년 3월까지이며, 시군구 단위의 지수를 사용하였다.
Ⅳ. 분석 결과
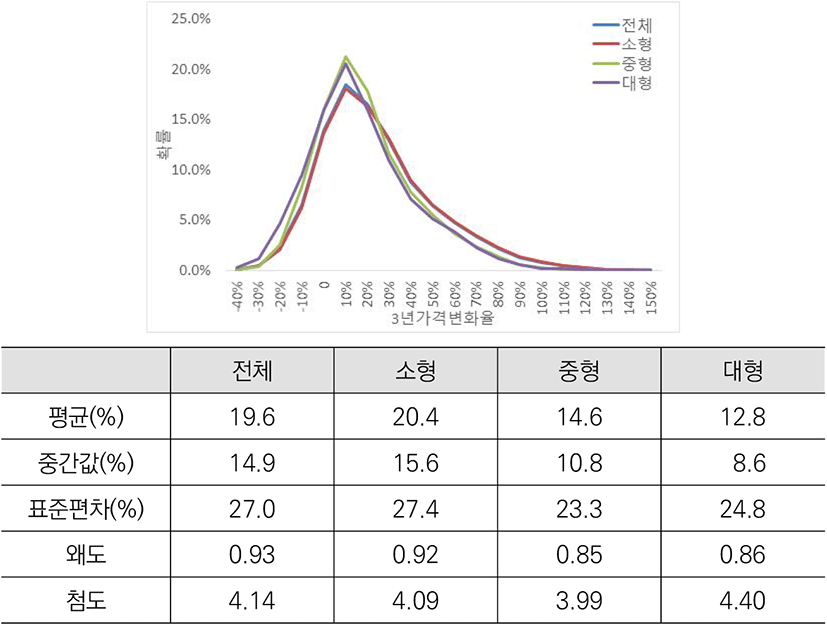
<그림 1>은 전체 및 크기별 비조건부 분포를 나타낸다. 분석기간 임의의 시점에 발생한 주택 매매거래로 취득한 주택을 3년 동안 보유했을 시 평균 19.6%의 가격 상승을 경험했을 것으로 나타났다. 분포의 모양은 왜도가 0보다 커 꼬리가 오른쪽으로 긴 모양을 나타내고 있으며, 따라서 중간값은 14.9%로 평균값보다 낮다. 첨도 또한 정규분포의 첨도가 3인 점을 고려하면, 4에 가까운 값을 가진다는 점은 극단적인 가격 변화율이 발생할 확률이 다소 높은 편임을 시사한다.
극단적인 가격 변화율이 발생할 확률이 정규분포에 비해 높은 특성은, 이론적으로 계산한 전월세전환율과 실제 세상에서 관찰되는 값 간의 차이를 일부 설명할 가능성이 있다. 안세륭 외(2020)는 임대인의 부도 리스크를 반영한 구조적 모형을 이용하여 전월세전환율의 특성을 분석하였는데, 정규분포의 가정을 이용한 계산 결과 전세가율 60% 이전에는 약 3.3% 수준, 전세가율 90%를 넘어가는 지점까지도 5% 수준이 나와, 당시 실제 세상에서 관찰되는 3%~8%와는 상당한 차이를 보였다. 물론 이들의 목적 자체가 실제 전월세전환율을 그대로 재현하는 것이 아닌 주요 요인들의 변화에 따른 전월세전환율의 변화를 분석하는 데 있었다는 점을 고려할 필요는 있을 것이다. 하지만 적지 않은 차이인 것만은 분명한데, 이 차이는 이들이 사용한 정규분포의 가정이 현실에 부합하지 않는다는 점과 관련이 있을 수 있다. 이 연구의 결과와 같이 실제 극단적인 가격 변화율이 발생할 확률이 정규분포보다 크다면, 임대인 입장에서는 이를 전월세전환율에 반영하고자 할 것이고, 결국 균형 전월세전환율은 높아질 것이다. 이에 대한 구체적인 분석은 후속 연구가 필요하다.
크기별 분포를 비교해 보면, 소형 주택의 평균 가격 상승률과 변동성이 높은 것으로 나타난다. 평균 가격 상승률은 소형(20.4%)>중형(14.6%)>대형(12.8%)인데 반해 표준편차는 소형(27.4%)>대형(24.8%)>중형(23.3%)으로, 대형주택의 가격 변동성이 상대적으로 높은 것으로 해석된다. 다만, 일반적인 주식 가격 상승률의 표준편차는 한 주식의 가격 시계열에 대한 가격 변동성을 의미하지만, 여기서는 각 크기별 주택의 횡단면적 가격 변동성 표준편차에 가까워 해석에 주의가 필요하다.
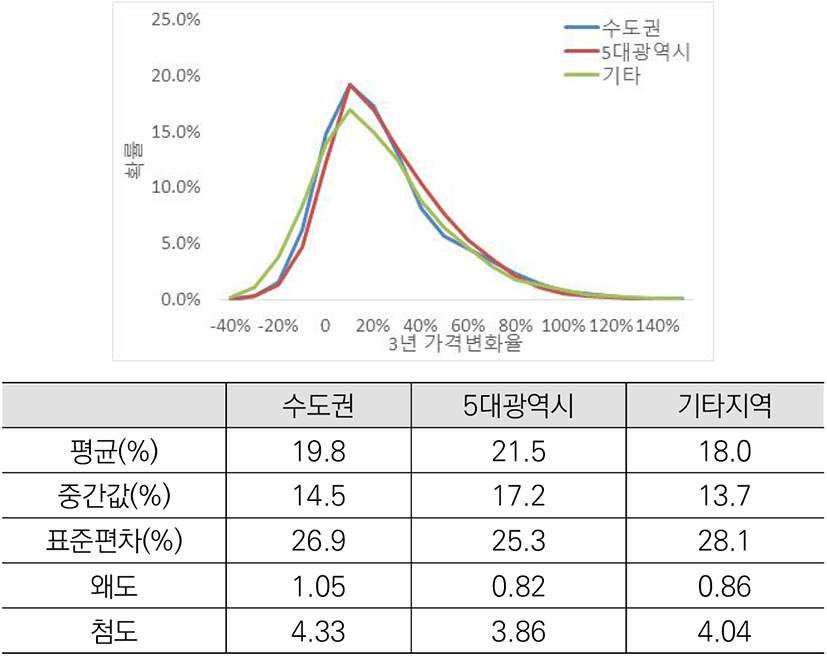
지역별로 나눠보면 5대광역시의 평균 가격 상승 폭이 가장 높은 반면 가격 상승률의 편차는 기타지역이 가장 높았다(<그림 2> 참조). 평균 가격 상승률은 5대광역시(21.5%)>수도권(19.8%)>기타지역(18.0%)이었다. 표준편차는 기타지역(28.1%)이 가장 컸고, 그 다음으로는 수도권(26.9%)과 5대광역시(25.3%)순이었다. 기타지역은 낮은 평균 가격 상승폭에 비해 변동성이 컸고 5대광역시는 변동성이 낮은 채로 높은 가격 상승폭을 보였다.
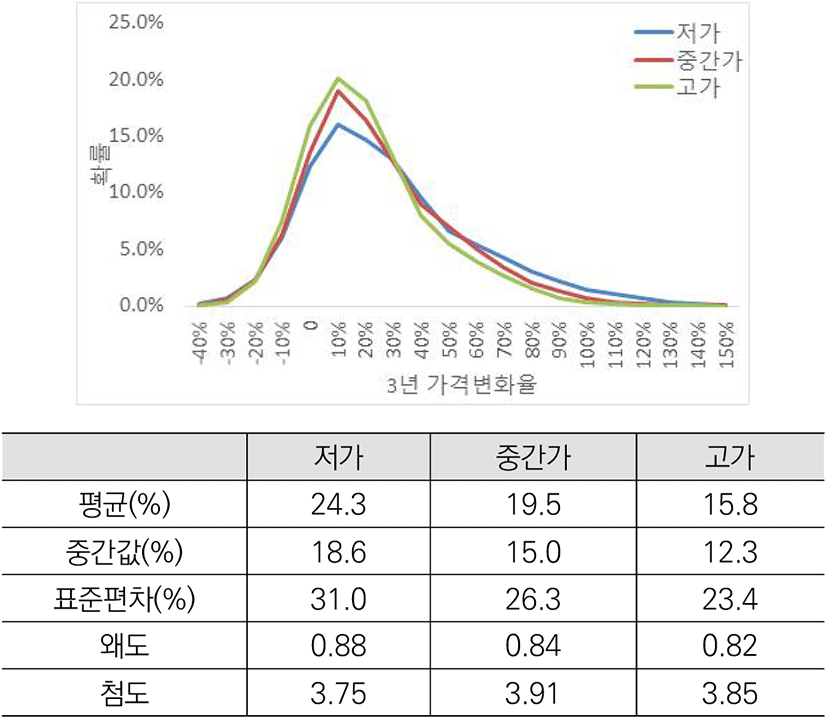
가격대별로 나눠보면 저가 주택이 고가 주택보다 약 8.5% 높은 평균 가격 상승률을 보였다(<그림 3> 참조). 단순히 전체 주택 중·저가 주택을 뽑는다면 대부분 소형, 기타지역의 주택이 이에 포함되어 앞선 분류와 겹치게 되지만, 여기서는 각 지역별, 면적대별 저가/중간가/고가 주택을 나누었으므로 앞선 분류와 겹치지 않는다. 평균 가격 차이만 놓고 보면 앞선 크기별, 지역별 차이보다 고가-저가 차이가 더 큰 것으로 나타난다. 하지만 중간값 차이는 6.3%로 이보다 소폭 작아, 앞선 소형-대형의 가격 변동률 중간값 차이인 7.0%보다 다소 작다.
앞선 비조건부 분포는 분석기간 전체에 대한 분포로, 주택가격 상승기와 하락기를 구분하지 않는다. 조건부 분포는 지역별 매매가격지수 변화율 구간별로 표본을 모아 분포를 만들어, 전체적인 가격이 상승하는 시기의 분포와 하락하는 시기의 분포를 나누어 볼 수 있다.
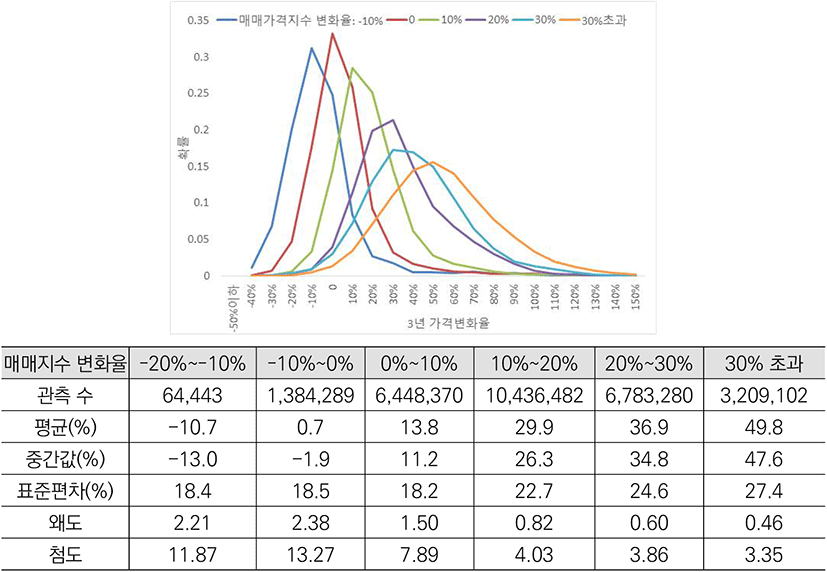
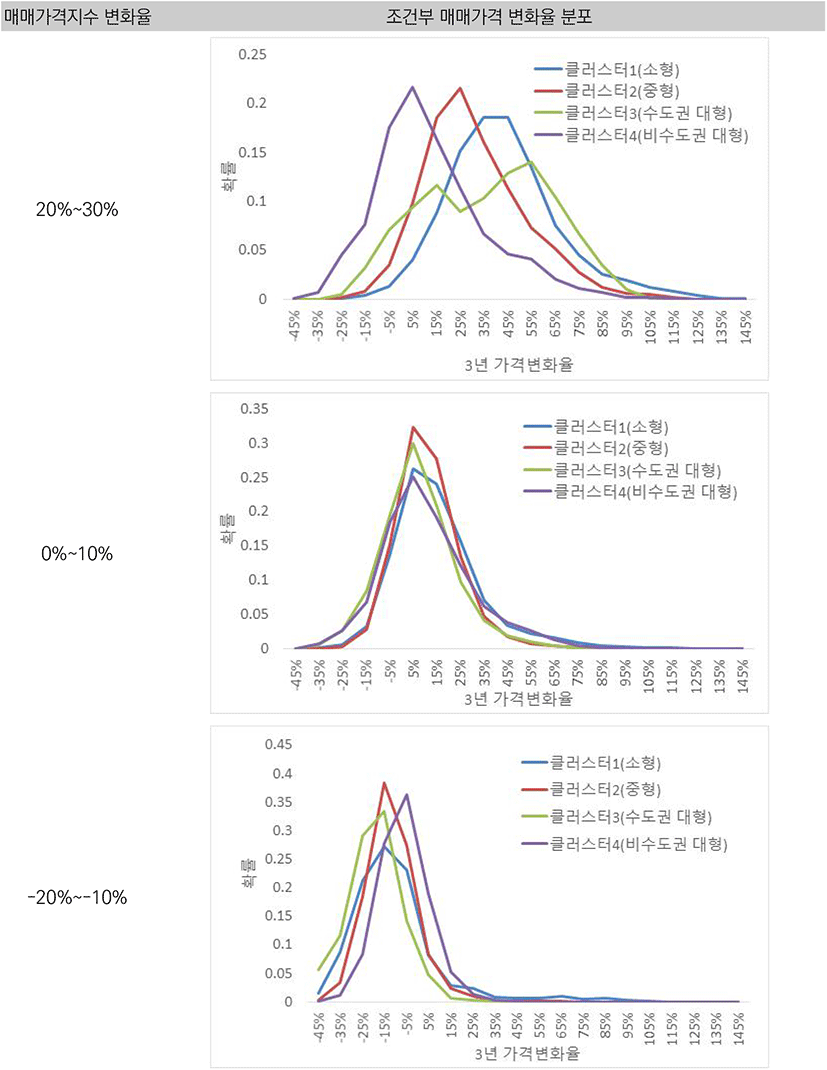
매매가격지수 변화율에 대한 조건부 분포는 <그림 4>에 나타냈는데, 매매가격 상승률 수준별로 분포의 모양이 상당히 다른 것을 확인할 수 있다. 매매가격지수 변화율이 −20%~−10%일 때는 분포의 모양은 대체로 좁은 모습을 보이는 반면, 매매가격지수 변화율이 높을수록 조건부 분포의 모양은 좌우로 넓게 퍼진 모습을 보인다. 이는 주택가격 하락기에는 다 같이 내리는 반면 상승기에는 차별적으로 오른다는 것을 의미한다. 또 한 가지 특징은, 주택매매가격지수 상승률이 높을 때는 왜도가 낮아 좌우대칭에 가까운 모습을 보이는 반면 가격 상승폭이 낮거나 하락할 때는 왜도가 크다는 점이다. 이에 따라 매매가격지수가 10%~20% 하락할 때 개별 거래 건의 평균 가격 하락폭은 10.7%인 반면 중간값은 13.0%이다. 이는 특히 주택가격 하락기에 평균 가격 변화율로 전체 분포를 설명할 경우 체감 현실과의 괴리가 높아질 수 있다는 것을 의미한다.
또한, 주택매매가격지수가 상승할 때도 오히려 주택가격이 하락하는 경우를 관찰하고 정량적으로 측정할 수 있다. 매매가격지수가 0%~10% 상승할 때는 18,5%가, 10%~20% 상승할 때는 5.2%가 가격 하락을 경험하였다.
앞서 지역별, 크기별, 가격대별로 평균 가격 상승률과 변동률에 차이가 있다는 것을 확인하였다. 세 요인이 모두 유의하므로 이를 동시에 고려하여 분포를 살피는 것이 이상적이겠으나, 지역별(3)×크기별(3)×가격대별(3)로 27가지의 분포가 만들어지며, 조건부 분포를 따지기 위해 매매가격지수 변화율 구간 6개를 사용한다면 27×6=162개의 분포가 만들어져, 이를 일일이 살펴보는 것은 매우 비효율적이다. 이에 이 절에서는 162개 분포를 이용해 유사한 분포의 모양을 보이는 주택 특성끼리 클러스터링을 하여 분석한다.
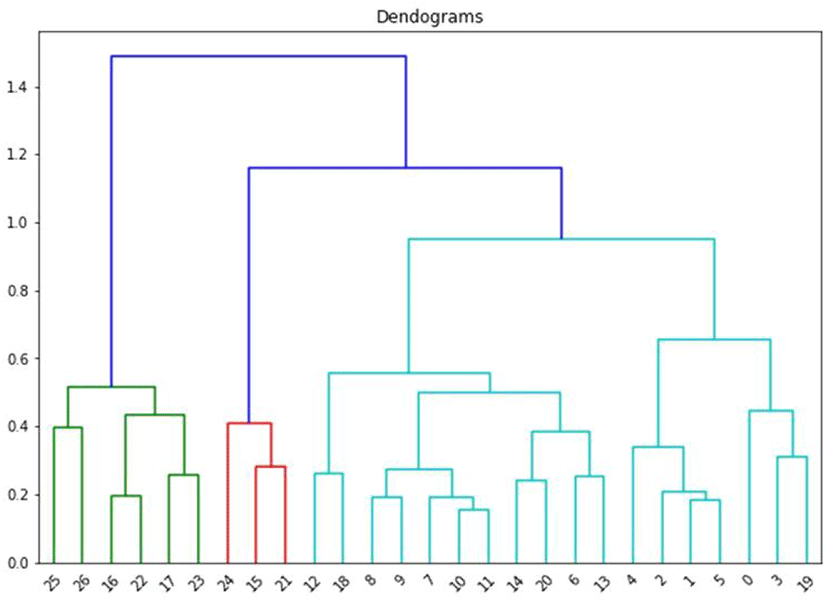
<그림 5>는 주택 특성별 분포의 유사도를 보여주는 댄도그램을 나타낸다. 세로줄의 길이가 길수록 다른 분포와의 유사도가 낮다는 것을 의미한다. 계층적 군집분석은 모든 표본을 가장 유사한 것끼리 하나씩 묶기 시작해서 궁극적으로는 모든 표본을 하나로 묶게 된다. 댄도그램을 살펴보면 분포를 4개로 나눌 때까지는 클러스터 간 차이가 상당히 존재하나, 5번째 클러스터는 기존 클러스터와 큰 차이가 없는 것을 확인할 수 있다. 따라서 이후부터는 4개의 클러스터로 나눈 결과를 설명한다.
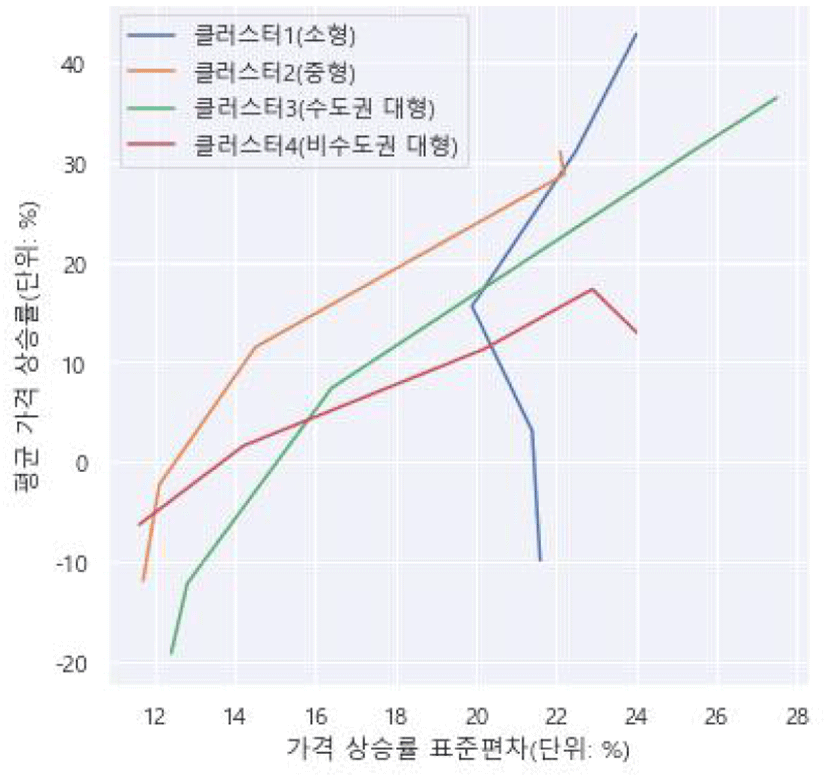
클러스터링 결과를 살펴보면 소형, 중저가 중심의 클러스터1; 중형, 평균적인 주택의 클러스터2; 수도권, 중대형, 중고가 중심의 클러스터3; 비수도권, 중대형, 고가 중심의 클러스터4로 나뉘는 것을 볼 수 있다(<표 6> 참조). 평균 가격 변화율은 <표 7>, 변화율의 표준편차는 <표 8>에 나타내었으며, 평균값과 표준편차의 관계는 <그림 6>에 나타내었다. 클러스터별 조건부 매매가격 변화율 분포의 그래프는 <그림 7>에 나타내었다.
| 매매가격지수 변화율 | −10% | 0% | 10% | 20% | 30% |
|---|---|---|---|---|---|
| 클러스터1(소형) | −9.9 | 3.1 | 15.6 | 31.2 | 42.9 |
| 클러스터2(중형) | −11.9 | −2.3 | 11.5 | 28.8 | 31.1 |
| 클러스터3(수도권 대형) | −19.2 | −12.2 | 7.4 | 31.4 | 36.5 |
| 클러스터4(비수도권 대형) | −6.3 | 1.6 | 11.3 | 17.3 | 13.0 |
| 매매가격지수 변화율 | −10% | 0% | 10% | 20% | 30% |
|---|---|---|---|---|---|
| 클러스터1(소형) | 21.6 | 21.4 | 19.9 | 22.5 | 24.0 |
| 클러스터2(중형) | 11.7 | 12.1 | 14.5 | 22.2 | 22.1 |
| 클러스터3(수도권 대형) | 12.4 | 12.8 | 16.4 | 25.5 | 27.5 |
| 클러스터4(비수도권 대형) | 11.6 | 14.2 | 20.2 | 22.9 | 24.0 |
평균 가격 상승률은 대체로 앞서 살펴본 크기별, 가격대별 가격변화율 특성과 유사하게 소형, 중저가(클러스터1) 주택이 가장 높았다. 클러스터1의 평균 가격 상승률은 매매가격지수가 10% 하락하는 경우를 제외하면 모든 매매가격지수 변화율 구간에서 가장 높아, 매매가격지수가 10% 상승할 때는 15.6%, 20% 상승 시 31.2%, 30% 상승할 때는 42.9% 상승하였다.
비수도권의 대형주택(클러스터4) 역시 앞서 살펴본 결과와 같이 가격 변동성이 낮아, 주택가격 상승기에 덜 오르고 하락기에 덜 내리는 모습을 보였다. 매매가격지수가 30% 상승할 때 클러스터4의 평균 상승폭은 13.0%로 가장 낮았고, 매매가격지수가 10% 하락할 때의 평균 하락 폭은 6.3%로 역시 모든 클러스터 중 가장 낮았다.
하지만 수도권 대형 아파트가 중심이 된 클러스터3은 주택가격 상승기에는 높은 가격 상승률을, 주택가격 하락기에는 높은 가격 하락률을 경험하였다. 매매가격지수가 30% 오를 때 클러스터3은 평균 36.5% 상승하여 클러스터1 다음으로 많이 올랐으며, 매매가격지수가 10% 하락할 때는 19.2% 하락하여 가장 큰 하락 폭을 보였다. 이는 앞서 살펴본 지역별, 가격대별, 크기별 일반적인 특징과는 다른 모습으로, 수도권 지역의 대형, 고가 아파트는 다른 주택과는 다른 속성을 가지고 있을 가능성을 제시한다.
또 한 가지 특이한 점은 매매가격지수가 30% 상승할 때의 조건부 분포가 쌍봉 형태를 띤다는 것이다. 이에 따라 가격 상승률의 표준편차가 27.5%로 다른 클러스터보다 높다. 이는 주택가격 상승기에는 수도권 대형 주택 내에서도 상승 폭이 큰 주택과 그렇지 않은 주택으로 다시 나눌 수 있음을 시사하며, 앞선 결과와 더불어 수도권의 대형 주택은 다른 주택과 다른 특성을 지니므로 추후 추가적인 연구가 필요함을 의미한다.
위에서 언급한 클러스터별 가격 변동성의 특성은 <그림 6>을 통해 보다 직관적으로 살펴볼 수 있다. 일반 금융상품에 대한 평균-표준편차 평면도는 한 상품의 가격 변동성 대비 평균 가격 상승률을 나타내는 반면, 앞서 언급한 바와 같이 여기서의 표준편차는 가격 변화율이 횡단면적으로 얼마나 퍼져 있는지를 나타낸다. 모든 클러스터의 그래프가 대체로 우상향하는 것을 볼 수 있는데, 이는 대체로 평균적인 가격이 하락할 때는 예외 없이 다 같이 하락하는 반면 상승할 때는 같은 클러스터에 포함되었다 할지라도 가격 상승률의 편차가 크다는 것을 의미한다. 평균적인 가격이 상승할 때 가격 상승률의 편차가 커지는 특성은 대체로 크기가 작을수록 뚜렷하고 크기가 커질수록 약화되는데, 수도권 대형 주택 중심인 클러스터3은 중형 주택과 유사하게 평균 가격이 상승할 때 가격 상승률의 편차가 크다. 또한, 소형 주택은 예외적으로 평균적인 가격이 하락할 때도 가격 하락 폭의 편차가 크다는 특징이 관찰된다.
Ⅴ. 결론
주택시장을 다룬 대부분의 기존 연구들은 가격지수를 이용하여 주택가격을 분석하였다. 이는 주택가격의 전체 분포가 가격지수 하나로 적절히 표현될 때는 합리적인 선택이다. 하지만 주택가격지수가 가지는 핵심적인 정보는 가격 수준이 아닌 변화율인데, 이제껏 가격지수가 주택가격 변화율의 분포를 얼마나 잘 대표하는지에 대한 검증은 이루어지지 않았다.
본 연구에서는 실거래 자료를 기반으로 주택가격의 패널데이터를 구축하고, 이를 이용해 주택가격 변화율의 분포를 도출하였다. 뿐만 아니라, 전반적인 주택가격이 상승하는 시기와 하락하는 시기별로 가격 변화율 분포를 도출하여, 주택시장의 다양한 측면에 대한 이해를 높이고자 하였다.
이를 통해 얻은 중요한 결론은 첫째, 주택가격 변화율 분포는 왜도가 0보다 커 꼬리가 오른쪽으로 긴 모습을 보이므로 중간값이 평균값보다 작다. 이는 주택가격지수의 변화율이 평균적인 주택가격 변화율을 나타낸다면 시장참여자들이 체감하는 시장과의 괴리를 나타낼 수 있다는 것을 의미한다. 특히, 주택가격 상승기에 비해 하락기에 왜도가 더 커져, 그 괴리는 주택가격 하락기에 더 커진다고 볼 수 있다.
둘째, 주택가격 하락기에는 개별 주택가격이 같이 하락하고 주택가격 상승기에는 차별적으로 상승한다. 이는 주택가격 하락기에는 가격 변화율 분포가 좁은 모습을 보이는 반면 상승기에는 넓게 퍼진 모습을 보인다는 점을 통해 내릴 수 있는 결론으로, 첫 번째 발견과 더불어 주택가격 상승기에는 주택가격지수의 상승률만으로는 주택시장의 가격 변화를 대표하기 어렵다는 것을 의미한다. 또한, 주택가격 하락기에 개별 주택가격이 같이 하락한다는 것은 가격 하락의 상관관계가 높다는 것으로, 유한책임대출 등 주택가격 기반 금융상품의 경우 일반적인 분포를 가정하였을 때보다 극단적인 손실이 발생할 확률이 높다는 것을 의미한다.
셋째, 주택가격지수가 상승할 때에도 가격이 하락하는 주택의 비중을 정량적으로 계산하였다. 계산 결과에 따르면 주택 구입 이후 매매가격지수가 3년간 0%~10% 상승할 때는 18.5%가, 10%~20% 상승할 때는 5.2%가 가격 하락을 경험하였다. 이러한 특징은 주택가격지수만을 이용한다면 정량적으로 측정하기 힘든 현상으로, 본 연구의 결과는 실제 현실을 보다 잘 반영할 뿐 아니라 유한책임대출과 같은 주택가격 기반 금융상품의 리스크를 측정할 때 필수적이다.
마지막으로, 수도권의 중·대형, 중·고가 주택은 본 연구에서 발견한 주택들의 일반적인 특성에서 벗어난 높은 변동성을 보인다. 분석 결과 일반적으로 주택의 크기가 작을수록, 가격대가 낮을수록 높은 가격 변동성을 보였다. 하지만 수도권의 중·대형, 중·고가 주택은 주택가격 상승기에는 평균보다 높은 상승 폭을, 하락기에는 평균보다 높은 하락 폭을 보였다. 이는 해당 주택을 거래하는 시장참여자들의 특성이 나머지 시장과는 다르다는 것을 시사하나, 정확한 원인에 대하여는 추가적인 연구가 필요하다.
이 연구의 의의는 주택가격의 패널데이터를 통하여 최초로 주택가격의 변동성 분포를 분석하였다는 점에 있다. 주택가격지수만을 이용해서 주택시장의 가격 변화를 분석한 기존 연구와는 달리, 지수가 대표하는 분포 전체에 대한 분석을 시도한 연구로서 기존 방식으로는 정량적으로 표현하거나 설명하기 어려웠던 주택시장의 특성들을 설명하였다. 이를 통해 이론적으로 계산된 전월세전환율과 실제 관측되는 전월세전환율 간의 차이를 일부 설명할 수 있는 가능성을 제기했으며, 실무적으로는 유한책임대출의 위험성을 정량적으로 계산할 수 있는 틀과 시나리오별 스트레스 테스트 수행에 필요한 가격 변화율 분포를 제시하였다.
하지만 이 연구는 전체 재고주택에 대한 고려 없이 단순히 실거래 정보만을 이용해 계산된 것으로, 이 연구의 결과만으로 주택가격지수가 가격 변화율 분포를 얼마나 잘 대표하는지 설명하는 데는 한계가 있다. 이 연구에서 계산한 비조건부 분포는 분석기간 발생한 주택매매거래로 취득한 주택을 3년간 보유했을 시 경험했을 주택가격 변화율의 분포를 의미하며, 이는 거래가 빈번한 주택을 좀 더 잘 대표한다. 주택가격지수와의 직접적인 비교를 위해서는 전체 재고주택에 대한 표본 혹은 전수 자료를 이용한 가격 변화율 분포를 생성해야 한다. 또한, 1/2층과 그 이상의 층별 가격 차이를 모두 무시하여 생길 수 있는 잠재적 오차에 노출되어 있다.
또한, 이 연구의 결과는 가격 및 가격 변화율의 실질값이 아닌 명목값을 사용하였다는 한계가 있다. 유한책임대출의 손실률을 추정하는 것과 같이 실제 위험관리에서는 명목값을 사용하지만, 보다 학술적인 분석에서는 실질값을 이용한다는 점을 고려하면 이 연구의 결과를 해석할 때는 이러한 점을 고려해야 할 것이며, 이러한 한계들을 보완하기 위해서는 추후 추가적인 연구가 필요하다.